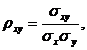Directional error

Introduction

In many theoretical considerations, as well as the navigation is necessary for practical applications on the accuracy of linear objects based on accurate information about their respective points. On the basis of knowledge (measurement) vector of random parameters calculated scalar, as a component of these vectors. An example is the calculation of the distance between two points whose coordinates (two or more dimensions) are defined on the basis of measurement. We also have a similar situation when the measured position coordinates define the location of spatial objects line - isobath, the edge of the quay or the fairway, a line restricting water body, distance to hazards, etc. In such situations, we should use the error code, rather than the average circular error.

Determining the dependence of error code (in the direction specified by the angle a, X-axis) is as follows:

Probability corresponding directional error is equal to the average probability of error (P = 0.683). Geometric interpretation of the error code is illustrated in the drawing below

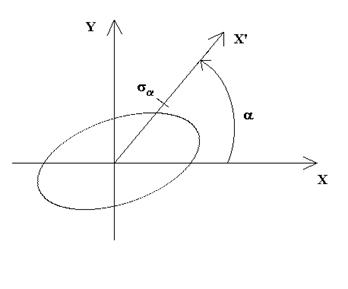
Fig. 1. Error in direction

Average error position equivalent to M is given by the formula

Between the average error of circular, elliptical semi axes average error and error code occur the following inequality:

Task:

Calculate and plot the average position error and error code in the function of the angle changes and the volatility of 0-360

Assuming that we define the position of a navigation system for which:

s_x=100 [m]

sy=25 [m]

s_xy=1600 [m²]

The correlation coefficient calculated by the formula