Objective: Shifting the coordinates on the surface of the rotational ellipsoid

Description:

Classic problem of calculating the coordinates on the surface of the ellipsoid of rotation, and azimuth and length of line is called the geodetic coordinates of the transfer. There are two types of problem: the so-called. Direct shifting and reverse shifting.

Task 1 - (direct shifting) consists in calculating the geodetic coordinates B2 L2 P2 and the geodetic azimuth line when the data are the coordinates of point P1 B1, L1, the length of the geodesic s and azimuth A of the geodesic line which starts from the point of P.

Task 2 - (reverse shifting) refers to the calculation of the length of the geodesic connecting the surface are ellipsoids two points with known coordinates of P1 and P2 and the calculation of the geodetic azimuth lines (straight and vice versa)

Example calculation method:

Among the several methods of calculation will be presented method of the average width of the Gaussian-task directly (Fig. 1.) Ranking calculations performed according to an algorithm (Fig.2.), Where B=j, L=l by the signs of surveying. Calculate the coordinates of the transfer must be made with the established minimum accuracy (table 1). This condition requires an iterative calculations. Suppose that in this example the condition is met in the second approximately.

Tab.1. Precision requirements:

•30-100 km: coordinates ±0.0001”, azimuth ±0.001”

•Do 1000 km: coordinates ±0.001”, azimuth ±0.01”

•Do 20 000 km: coordinates ±0.003”, azimuth ±0.03”

•

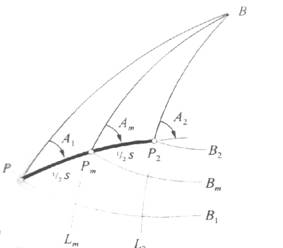
Fig.1. The method of the average latitude of the Gaussian

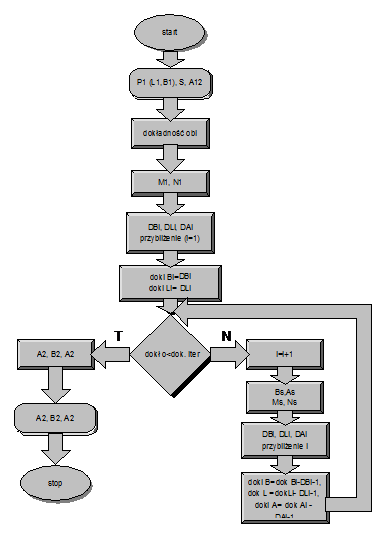
Fig.2. Algorithm

Formulas as follow:

First iteration as follow

, where

, where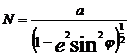

where:

r”=206264.8062 – radian expressed in seconds

t²=tg²j_s

Second iteration as follow

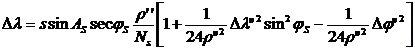
Example:

Ellipsoid WGS-84

A	6378137
e^2	0.006694438
e’^2	0.0673949674227

Initial data

A=315^o

S=200000

Result

A2=134.41^o