Tworząc niniejszą stronę wykorzystałem m. in. treści
Treichel W. Ćwiczenia z Visual Basic,
Mikom, Warszawa 2001
Uzupełnieniem operatorów w VB są funkcje umożliwiające
wykonywać wiele operacji. Oto kilka z nich wraz z wyjaśnieniem i składnią
Wyprowadzone funkcje matematyczne
Funkcje łańcuchowe
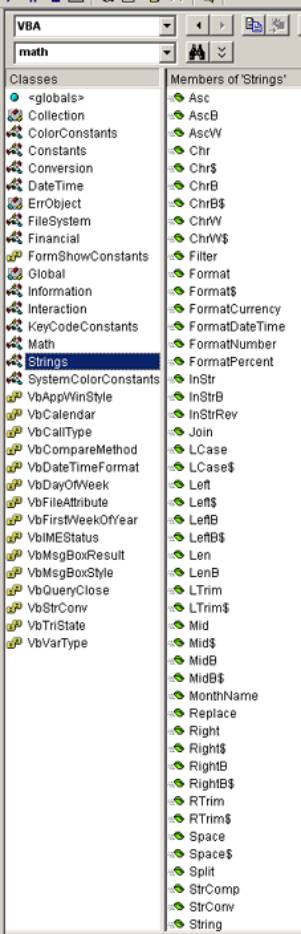
Len
zwraca wartość zawierającą liczbę znaków łańcucha
Len(łancuch)
Left
zwraca łańcuch (String) zawierający określoną liczbę
znaków od lewej strony łańcucha.
Składnia
Left(Łańcuch, Długość)
Right
zwraca łańcuch (String) zawierający określoną liczbę
znaków od prawej strony łańcucha.
Składnia:
Right(Łańcuch, Długość)
Mid
zwraca łańcuch (String) zawierający określoną liczbę
znaków z łańcucha.
Składnia:
Mid(Łańcuch, Początek ,Długość)
InStr
zwraca wartość określającą pozycję jednego łańcucha
w drugim.
Składnia funkcji
InStr([Początek,] Łańcuch1, Łańcuch2 [Porównanie])
UCase
zwraca łańcuch (String) przekonwertowany na duże
litery.
Składnia
UCase(Łańcuch)
Lcase
zwraca łańcuch (String) przekonwertowany na małe
litery.
Składnia funkcji
LCase(Łańcuch)
Funkcje przekształcające
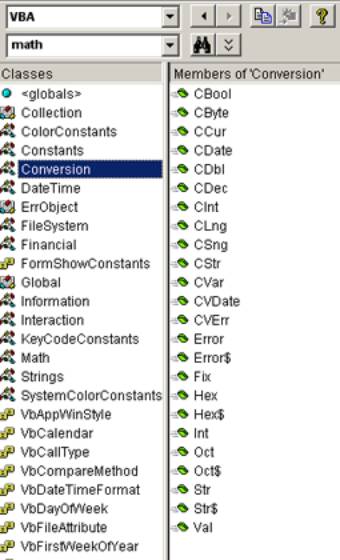
Int(x)
Zwraca część całkowitą liczby nieujemnej, a z liczby
ujemnej najbliższą całkowitą liczbę mniejsza od x
Fix(x)
Zwraca całkowitą część liczby nieujemnej, a dla
ujemnych cześć całkowitą po obcięciu części ułamkowej
Funkcje Matematyczne:
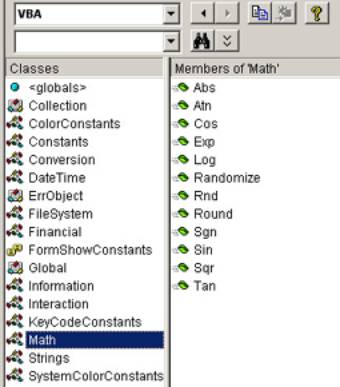
Abs
Funkcja Abs zwraca wartość bezwzględną
podanej wartości.
Składnia
Abs(wartość)
Argument Wartość jest wymagany. Może to być
dowolne wyrażenie numeryczne. Jeżeli argument Wartość ma wartość Null, to
zostanie zwrócona wartość Null. Jeżeli jest to niezainicjowana zmienna,
zostanie zwrócone zero.
Wartość bezwzględna liczby to liczba bez znaku. Np.
Abs(1) i Abs(-1) zwracają wartość 1.
Przykład użycia funkcji Abs:
zmienna=Abs (8) {zmienna przyjmuje wartość 8}
zmienna=Abs(-8){zmienna przyjmuje wartość 8}
Atn
Funkcja Atn zwraca wartość funkcji arcus
tangens (typu Double) podanej wartości.
Składnia:
Atn(Wartość)
Argument Wartość jest wymagany. Może być typu
Double lub dowolnym wyrażeniem numerycznym.
Zakres wyników funkcji Atn jest od -pi/2 do
pi/2 radianów.
Cos
Funkcja Cos zwraca wartość cosinusa podanego
kąta.
Składnia funkcji Cos:
Cos(Wartość)
Argument Wartość jest wymagany. Może być typu
Double lub dowolnym wyrażeniem numerycznym określającym kąt w radianach.
Zakres wyników funkcji Cos: -1 do 1.
Exp
Funkcja Exp zwraca wartość stałej e (podstawy
logarytmu naturalnego) podniesionej do podanej potęgi. Zwracana wartość jest
typu Double.
Składnia
Exp(Potęga)
Argument Potęga jest wymagany. Może być typu Double
lub dowolnym wyrażeniem numerycznym.
Log
Funkcja Log zwraca wartość logarytmu
naturalnego podanej liczby w postaci wartości typu Double.
Składnia:
Log(Wartość)
Argument Wartość jest wymagany. Może być typu
Double lub dowolnym wyrażeniem numerycznym większym niż zero.
Jeżeli argument Wartość będzie miał wartość
mniejszą lub równą zero, zostanie wygenerowany błąd.
Można obliczyć logarytm o dowolnej podstawie n z
liczby x przez podzielenie logarytmu naturalnego z x przez logarytm naturalny z
podstawy n:
Logn(x) = Log(x) / Log(n)
Aby obliczyć logarytm o podstawie 10 można posłużyć
się zapisem:
Log10 = Log(X)/Log(10)
Rnd
Funkcja Rnd zwraca liczbę losową typu Single.
Składnia:
Rnd (Wartość)
Argument Wartość jest opcjonalny. Może być
typu Single lub dowolnym wyrażeniem numerycznym.
Wartości zwracane przez funkcję Rnd:
|
Wartość
wejściowa |
Zwracana
wartość |
|
Mniejsza
niż zero |
Ta
sama wartość za każdym razem (wartość wejściowa używana jako podstawa
generatora liczb losowych) |
|
Równa
zero |
Najczęściej
generowana liczba |
|
Większa
niż zero |
Następna
liczba losowa w sekwencji |
|
Nieokreślona |
Następna
liczba losowa w sekwencji |
Funkcja Rnd zwraca wartość mniejszą niż 1 i
większą lub równą zero.
Wartość argumentu Wartość określa sposób generowania
liczb przez funkcję Rnd:
Dla każdej podanej podstawy generatora zwracana jest
ta sama liczba przy każdym wywołaniu funkcji Rnd, ponieważ poprzednia
liczba jest używana jako podstawa generatora dla następnej liczby w sekwencji.
Przed wywołaniem funkcji Rnd należy użyć
instrukcji Randomize bez argumentów aby zainicjować generator pseudolosowy z
podstawą opartą na zegarze systemowym.
Aby powtórzyć sekwencję liczb losowych należy
wywołać funkcję Rnd z ujemnym argumentem bezpośrednio przez użyciem Randomize
z argumentem numerycznym. Użycie Randomize z tą samą wartością nie powtórzy
poprzedniej sekwencji.
Przykład użycia funkcji Rnd:
zmienna=Int((6*Rnd)+1) {wygenerowana wartość z zakresu 1 do 6}
Rozkaz Randomize
Instrukcja Randomize inicjuje generator liczb
pseudoloswych.
Składnia rozkazu Randomize:
Randomize [Wartość]
Argument Wartość jest opcjonalny. Może być
typu Variant lub dowolnym wyrażeniem numerycznym.
Randomize wykorzystuje podaną Wartość do zainicjowania
generatora liczb pseudolosowych funkcji Rnd(), używając ją jako podstawę
generatora. Jeżeli Wartość zostanie pominięta, zostanie wykorzystany
zegar systemowy jako podstawa generatora.
Jeżeli Randomize nie zostanie użyte, to
funkcja Rnd() (bez argumentów) będzie używać tej samej liczby jako podstawy
generatora jak przy pierwszym wywołaniu i będzie następnie używać ostatnio
wygenerowanej wartości jako podstawy generatora.
Aby powtórzyć sekwencję liczb losowych należy
wywołać funkcję Rnd() z ujemnym argumentem bezpośrednio przez użyciem Randomize
z argumentem numerycznym. Użycie Randomize z tą samą wartością nie
powtórzy poprzedniej sekwencji.
Przykład użycia rozkazu Randomize:
Randomize {zainicjowanie generatora}
Zmienna =Int((6*Rnd)+1) {wygenerowanie liczby z zakresu
1 do 6}
Sgn
Funkcja Sgn zwraca wartość typu Integer
określającą znak podanej wartości.
Składnia funkcji Sgn:
Sgn(Wartość)
Argument Wartość jest wymagany i może być
dowolnym wyrażeniem numerycznym.
Wartości zwracane przez funkcję Sgn:
|
Wartość
wejściowa |
Zwracana
wartość |
|
Większa
niż zero |
1 |
|
Równa
zero |
0 |
|
Mniejsza
niż zero |
-1 |
Znak argumentu Wartość określa wartość
zwracaną przez funkcję Sgn.
Przykład użycia funkcji Sgn:
zmienna=Sgn(10) {zmienna=1
zmienna =Sgn(0) {zmienna =0}
zmienna =Sgn(-10){zmienna=-1}
Sin
Funkcja Sin zwraca wartość cosinusa podanego
kąta.
Składnia funkcji Sin:
Sin(Wartość)
Argument Wartość jest wymagany. Może być typu
Double lub dowolnym wyrażeniem numerycznym określającym kąt w radianach.
Zakres wyników funkcji Sin: -1 do 1.
Sqr
Funkcja Sqr zwraca wartość pierwiastka
kwadratowego podanej wartości.
Składnia:
Sqr(Wartość)
Argument Wartość jest wymagany. Może być
dowolnym wyrażeniem numerycznym większym lub równym zero.
Jeżeli argument Wartość będzie miał wartość
mniejszą od zera, zostanie wygenerowany błąd.
Przykład użycia funkcji Sqr:
pierwiastek=Sqr(4) {wynik=2}
pierwiastek=Sqr(0) {wynik=0}
pierwiastek=Sqr(-4){błąd}
Tan
Funkcja Tan zwraca wartość funkcji tangens
podanej wartości.
Składnia:
Tan(Wartość)
Argument Wartość jest wymagany. Może być
dowolnym wyrażeniem numerycznym określającym wartość kąta w radianach.
Wyprowadzone funkcje matematyczne
|
Secant |
Sec(X) =
1 / Cos(X) |
|
Cosecant |
Cosec(X)
= 1 / Sin(X) |
|
Cotangent |
Cotan(X)
= 1 / Tan(X) |
|
Inverse
Sine |
Arcsin(X)
= Atn(X / Sqr(-X * X + 1)) |
|
Inverse
Cosine |
Arccos(X)
= Atn(-X / Sqr(-X * X + 1)) + 2 * Atn(1) |
|
Inverse
Secant |
Arcsec(X)
= Atn(X / Sqr(X * X – 1)) + Sgn((X) – 1) * (2 * Atn(1)) |
|
Inverse
Cosecant |
Arccosec(X)
= Atn(X / Sqr(X * X - 1)) + (Sgn(X) – 1) * (2 * Atn(1)) |
|
Inverse
Cotangent |
Arccotan(X)
= Atn(X) + 2 * Atn(1) |
|
Hyperbolic
Sine |
HSin(X) =
(Exp(X) – Exp(-X)) / 2 |
|
Hyperbolic
Cosine |
HCos(X) =
(Exp(X) + Exp(-X)) / 2 |
|
Hyperbolic
Tangent |
HTan(X) =
(Exp(X) – Exp(-X)) / (Exp(X) + Exp(-X)) |
|
Hyperbolic
Secant |
HSec(X) =
2 / (Exp(X) + Exp(-X)) |
|
Hyperbolic
Cosecant |
HCosec(X)
= 2 / (Exp(X) – Exp(-X)) |
|
Hyperbolic
Cotangent |
HCotan(X)
= (Exp(X) + Exp(-X)) / (Exp(X) – Exp(-X)) |
|
Inverse
Hyperbolic Sine |
HArcsin(X)
= Log(X + Sqr(X * X + 1)) |
|
Inverse
Hyperbolic Cosine |
HArccos(X)
= Log(X + Sqr(X * X – 1)) |
|
Inverse
Hyperbolic Tangent |
HArctan(X)
= Log((1 + X) / (1 – X)) / 2 |
|
Inverse
Hyperbolic Secant |
HArcsec(X)
= Log((Sqr(-X * X + 1) + 1) / X) |
|
Inverse
Hyperbolic Cosecant |
HArccosec(X)
= Log((Sgn(X) * Sqr(X * X + 1) + 1) / X) |
|
Inverse
Hyperbolic Cotangent |
HArccotan(X) = Log((X
+ 1) / (X – 1)) / 2 |
|
Logarithm
to base N |
LogN(X) = Log(X) / Log(N) |