Powierzchnie odniesienia

Kształty ziemi

Na kształt Ziemi wpływa wiele czynników: jej ruch obrotowy i obiegowy, cieplny i grawitacyjny wpływ ciał niebieskich, własności fizyczne litosfery i hydrosfery i wiele innych. Fizyczną powierzchnię Ziemi tworzą różnorodne formy ukształtowania powierzchni obszarów wodnych zwanych akwenami. Jednak powierzchnia akwenów nie ma stałego kształtu gdyż występują zmiany poziomu wód.

Precyzyjne ujęcie kształtów Ziemi zależy od ustalenia pewnej, prawidłowej, dającej się ująć matematycznie powierzchni najbardziej zbliżonej pod względem formy do rzeczywistego kształtu Ziemi, na którą można by dokonać pionowego rzutu jej powierzchni fizycznej. Powierzchnia tego rodzaju nazywa się powierzchnią odniesienia.

W zależności od prowadzonych badań oraz dokładności obliczeń (precyzji pomiarów) za powierzchnię odniesienia Ziemi przyjmuje się:

· Geoidę

· Elipsoidę

· Kulę

Rys. 1 Różnice pomiędzy powierzchniami odwzorowań

Fizyczna powierzchnia Ziemi jest bardzo skomplikowana i ma złożone kształty. Z tych względów ustalono pewien poziom, do którego odnoszą się pomiary rzeźby powierzchni Ziemi. Za taki poziom odniesienia przyjęto poziom mórz i oceanów przy pełnej równowadze znajdujących się w nich mas wodnych.

Kształt Ziemi został ustalony na podstawie wielu pomiarów. Na podstawie badań ruchu sztucznych satelitów Ziemi otrzymano następujące wielkości dużej półosi i spłaszczenia Ziemi [2]:

a = 6 378 153 m +/- 8 m

f = 1:298,25 +/- 0,01

Gdzie: a – duża półoś

f - spłaszczenie

1. Geoida

Najczęściej przyjmuje się, że Ziemia ma kształt geoidy. Geoida jest bryłą geometryczną, ograniczoną powierzchnią ekwipotencjalną, pokrywającą się z powierzchnią oceanów przy pełnej równowadze znajdujących się w nich mas wodnych. Niestety powierzchnia geoidy na skutek nierównomiernie rozmieszczonych mas we wnętrzu Ziemi nie jest regularna w sensie matematycznym, dlatego nie można jej uznać za odniesienie do pomiarów i przedstawienia ich wyników oraz obliczeń. Zważywszy na fakt, że około 71% powierzchni Ziemi pokrywają oceany, dojdziemy do wniosku, że geoida stanowi reprezentatywne przybliżenie kształtu Ziemi.

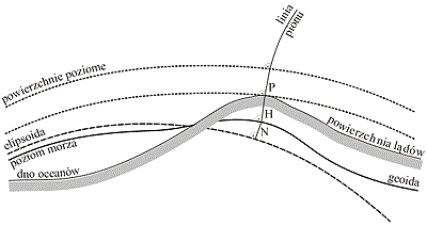
Rys.2 Powierzchnie Ziemi, elipsoida i geoida

2. Elipsoida obrotowa

Najprostszą bryłą matematyczną, najbardziej zbliżoną do kształtu geoidy, którą można opisać analitycznie jest elipsoida obrotowa. Jest to powierzchnia zamknięta, powstała z obrotu elipsy wokół małej osi symetrii.

Rozmiary i kształt takiej elipsoidy określają:

a – duża półoś, zwana równikową

b – mała półoś, zwana biegunową

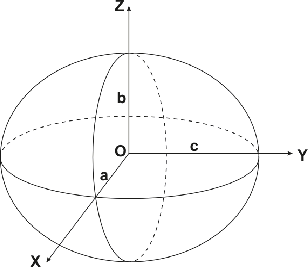
Rys. 3 Kształty i wymiary elipsoidy obrotowej

W praktyce wykorzystuje się również inne wielkości wyrażające wzajemny stosunek półosi, a zwłaszcza:

- biegunowe spłaszczenie elipsoidy (ƒ):

{1}

gdzie: a – duża półoś elipsy

b – mała półoś elipsy

- pierwszy mimośród (ekscentryczność)

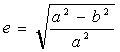{2}

- drugi mimośród (eliptyczność)

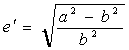{3}

Do jednoznacznego określenia elementów elipsoidy wystarcza znajomość dwóch z czterech wymienionych parametrów, przy czym jednym z nich winna być zawsze długość jednej z półosi.

Elipsoida o ustalonych wymiarach, zorientowana wewnątrz bryły ziemskiej tak, aby jej powierzchnia była najbardziej zbliżona do powierzchni geoidy, stanowi powierzchnię odniesienia. Orientowanie elipsoidy wewnątrz geoidy polega na odpowiednim jej umieszczeniu bądź względem powierzchni geoidy, bądź względem jej środka oraz na określeniu kierunków jej osi tak, aby powierzchnia elipsoidy była najbardziej zbliżona do powierzchni geoidy albo na wybranym obszarze (w lokalnych układach odniesienia), albo na całej powierzchni Ziemi (w globalnych układach odniesienia).

Wybrane parametry najbardziej znanych elipsoid odniesienia:

Tab. 1. Parametry wybranych elipsoid odniesienia

Elipsoida odniesienia	a [m]	b [m]	e²	1:f
EVEREST 1830	6377276,34	6356075,41	0,00663785	300,8017
BESSEL 1841	6377397,15	6356078,96	0,00667437	299,15281285
CLARKE 1866	6378206,4	6356583,8	0,00676866	294,9786982
HAYFORD 1909	6378388	6356911,946	0.00672267	297,00
KRASOWSKI 1940	6378245	6356863,019	0,00669342	298,3
WGS-72	6378135	6356750,52	0,00669432	298,26
WGS-84	6378137	6356752,314	0,0066943799901	298,25722356

3. Kula

W nawigacji, podobnie jak i niektórych innych dziedzinach wiedzy można przyjąć Ziemię jako kulę o promieniu równym 6370 km. Traktując ziemię jako kulę można w przybliżeniu wyznaczyć jej oś obrotu. Przyjmuje się, że jest to prosta. Punkty przebicia tej prostej z powierzchnią ziemi nazywa się biegunami, gdzie biegun północny oznacza się literą N, a południowy literą S. Płaszczyzna prostopadła do osi obrotu Ziemi i przechodząca przez jej środek nazywa się płaszczyzną równika. Płaszczyzna ta przecina się z powierzchnią kuli ziemskiej i tworzy koło wielkie zwane równikiem. Promień równika równy jest promieniowi kuli. Wszystkie płaszczyzny równoległe do płaszczyzny równika przecinają powierzchnię kuli wzdłuż kół małych, noszących nazwę równoleżników. Wszystkie płaszczyzny przechodzące przez oś obrotu Ziemi i prostopadłe do płaszczyzny równika przecinają kulę wzdłuż kół wielkich zwanych południkami.

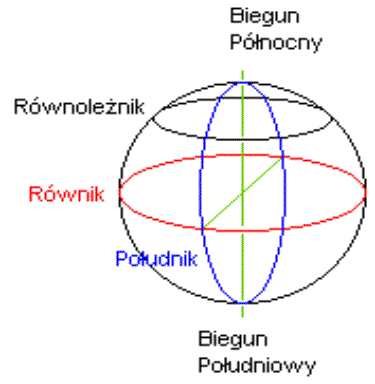
Rys.4. Kula ziemska

Jednak w rzeczywistości różnice między kulą a elipsoidą obrotową są niewielkie.

Kula spełniająca rolę elipsoidy obrotowej musi odpowiadać następującym warunkom:

- Powierzchnia kuli musi być równa powierzchni elipsoidy obrotowej

- Objętość kuli musi być równa objętości elipsoidy obrotowej

Objętość elipsoidy obrotowej V_e wynosi:

{4}

Objętość kuli V_k wynosi: