ELIPSOIDA ZIEMSKA I PODSTAWOWE ZALEŻNOŚCI WYSTĘPUJĄCE NA JEJ POWIERZCHNI

1. Charakterystyka elipsoidy jako powierzchni odniesienia.

1.3. Linia geodezyjna

1.4. Długość łuku południka.

1.5. Długość łuku równoleżnika.

2. Układy odniesienia i ich opis

2.1. Charakterystyka lokalnych układów odniesienia.

2.2.1.Układ północnoamerykański (NAD 27).

2.2.2 Układ europejski (ED 50).

2.2.3 Układ indyjski (IND).

2.2.4 Układ japoński (JAP).

2.2.5 Układ ‘42’ (URSS).

2.2.6 Układ południowoamerykański (SAD).

2.2.7 Układ afrykański (ARC).

2.2.8 Układ australijski (AND).

2.2.9 Układ argentyński (ARG).

2.2.10 Układ Hawajski (HAW).

2.2. Charakterystyka układów geocentrycznych.

1. Charakterystyka elipsoidy jako powierzchni odniesienia.

Ziemia ma kształt spłaszczonej elipsoidy, której półoś równikowa wynosi około 6373 km, półoś biegunowa około 6357 km. Fizyczną powierzchnię Ziemi w 71% tworzy powierzchnia mórz i oceanów, zaś w 29% powierzchnia lądów, przy czym wzniesienia tych ostatnich w stosunku do powierzchni oceanów mogą lokalnie osiągać kilka kilometrów.

Teoretyczną powierzchnią Ziemi jest powierzchnia geoidy, która pokrywa się z przedłużonym pod lądami średnim poziomem mórz i oceanów. Na tej powierzchni wartość potencjału siły ciężkości jest stała i równa potencjałowi na średnim poziomie mórz i oceanów. Ze względu jednak na niejednorodność mas Ziemi i ich niejednorodne rozmieszczenie w jej wnętrzu, powierzchnia geoidy ma kształt nieregularny (wzniesienia i zagłębienia) i nie jest w każdym punkcie analityczna. Z tego też powodu powierzchnia ta nie może być przyjęta za powierzchnię odniesienia stanowiącą jeden z elementów układu odniesienia.

Najprostszą bryłą matematyczną, najbardziej zbliżoną do kształtu geoidy jest elipsoida obrotowa, czyli powierzchnia zamknięta, powstała w wyniku obrotu elipsy wokół jednej z jej osi symetrii, w tym wypadku małej półosi.

Jednym z podstawowych zadań geodezji wyższej jest ustalenie wymiarów elipsoidy ziemskiej najbardziej zbliżonej do kształtu Ziemi, która spełniałaby następujące warunki:

· Środek elipsoidy powinien pokrywać się ze środkiem ciężkości Ziemi, a płaszczyzna jej równika z płaszczyzną równika Ziemi,

· Objętość elipsoidy powinna być równa objętości geoidy,

· Suma kwadratów odchyleń geoidy od elipsoidy powinna być minimalna.

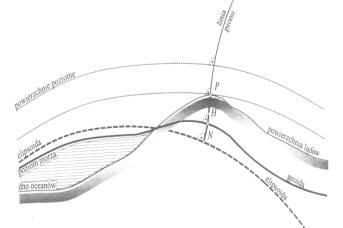
Rys. 1 Powierzchnia odniesienia: geoida i elipsoida.

Góra strony

1.1. Parametry opisujące elipsoidę

Elipsoidą nazywamy powierzchnię o równaniu kanonicznym:

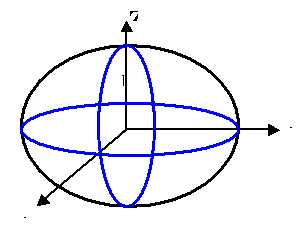
Rys. 2 Elipsoida.

Liczby a, b, c nazywamy półosiami elipsoidy

Jeśli półosie a i c są sobie równe (a = c) to elipsoidę nazywamy elipsoidą obrotową.

Rozmiary i kształt elipsoidy określają następujące elementy:

a – duża półoś, zwana równikową,

b – mała półoś, zwana biegunową.

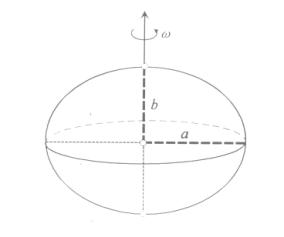
Rys. 3. Elipsoida obrotowa.

W praktyce wykorzystuje się również inne wielkości wyrażające wzajemny stosunek półosi, a zwłaszcza:

· Biegunowe spłaszczenie elipsoidy (f lub a)

gdzie:

f – biegunowe spłaszczenie elipsoidy,

a - duża półoś, zwana równikową,

b - mała półoś, zwana biegunową.

Niekiedy f nazywamy spłaszczeniem elipsy południkowej, tzn. takiej, jaka powstaje w wyniku przekroju elipsoidy płaszczyzną zawierającą małą półoś b.

· Pierwszy mimośród elipsoidy (e):

· Drugi mimośród elipsoidy (e’):

· Można łatwo wykazać następujące, ważniejsze związki pomiędzy parametrami elipsoidy obrotowej:

gdzie:

e - pierwszy mimośród elipsoidy,

f = 1 - = 1-,

( 1-e² ) * ( 1+e’²) = 1,

e’² =, e²= ,

e^2
=2f – f², e²2f,

gdzie:

f – biegunowe spłaszczenie elipsoidy,

a - duża półoś, zwana równikową,

b – mała półoś, zwana biegunową,

e² - kwadrat pierwszego mimośrodu elipsoidy,

e’² – kwadrat drugiego mimośrodu elipsoidy.

Równanie powierzchni elipsoidy obrotowej, wyrażone przez współrzędne prostokątne, podaje się zazwyczaj w postaci:

gdzie:

x, y, z – przestrzenne współrzędne prostokątne,

Wprowadziwszy oznaczenia:

albo ,

równanie elipsoidy zapisujemy również w postaci:

x²+ y² +z²= a².

Elipsoida obrotowa jest określana przez dwa parametry, w tym przynajmniej przez jeden długościowy, np. a i b lub przez półoś a i spłaszczenie a. Parametry te muszą mieć przyjęte wartości liczbowe, które otrzymuje się na podstawie odpowiednich pomiarów geodezyjnych. Tak w wyniku opracowania pomiarów wyznaczone zostały elipsoidy np. Everesta (1830 r.), Bessela (1841 r.), Clarke’a (1866 r.), Hayforda (1909 r.), Krasowskiego (1940 r.) oraz wiele innych wcześniejszych i późniejszych elipsoid.

Na kongresie Unii Geodezyjno-Geograficznej w 1924 roku w Madrycie elipsoida Hayforda została przyjęta jako międzynarodowa i zalecono ją do stosowania także w pracach o charakterze globalnym. W działaniach o mniejszym zasięgu, na przykład w wielu krajowych sieciach geodezyjnych nadal są używane już wcześniej przyjęte elipsoidy.

W roku 1940 zostały opublikowane w ZSRR parametry elipsoidy Krasowskiego, oparte na bardzo obszernym własnym nowym materiale pomiarowym oraz na badaniach wielu innych krajów europejskich i amerykańskich (USA, Kanada). Elipsoida Krasowskiego w 1942 roku została przyjęta we wszystkich pracach geodezyjnych w ZSRR. W Polsce i w innych krajach demokracji ludowej wprowadzono ją w 1956 roku jako elipsoidę odniesienia. Wybór ten jest jedynie w pewnym sensie i w pewnych granicach sprawą obojętną. Decydują o nim zwykle względy praktyczne, na przykład przyjęcie elipsoidy w krajach sąsiednich. Należy jednak pamiętać, że nawet wspomniana sytuacja nie musi prowadzić do jednolitych układów odniesienia współrzędnych, gdyż te ostatnie związane są jeszcze z tzw. punktem przyłożenia elipsoidy i z jej orientacją.

Wybrane parametry (a, b, 1/f, e² – odpowiednio duża i mała półoś, odwrotność biegunowego spłaszczenia, kwadrat pierwszego mimośrodu) ośmiu najbardziej znanych elipsoid odniesienia przedstawiono w tabeli 1. Dla każdej z nich podano również te układy odniesienia współrzędnych, w których dana elipsoida została przyjęta za powierzchnię odniesienia.

Tabela 1. Parametry ellipsoid

Lp	Nazwa i rok	Duża półoś a	Mała półoś b	Odwrotność	Kwadrat	Układy odniesienia współrzędnych
	określenia	[ m ]	[m ]	biegunowego spłaszczenia 1/f	Pierwszego mimośrodu e²
	elipsoidy			spłaszczenia 1/f	mimośrodu e²
1	Everest –1830	6377276.345	6356075.413	300.802	0.00663785	IND
2	Bessel – 1841	6377397.155	6356078.963	299.153	0.00667437	JAP
3	Clarke – 1866	6378206.400	6356583.800	294.979	0.00676866	NAD 27
3	Clarke – 1866	6378206.400	6356583.800	294.979	0.00676866	HAW
4	Clarke zmodyfikowany – 1880	6378249.145	6356514.870	293.465	0.00680351	ARC
5	Hayford –1909	6378388.000	6356911.946	297.000	0.00672267	EUR (ED-50)
6	Krasowski –1940	6378245.000	6356863.019	298.300	0.00669342	URSS (‘42’)
7	Międzynarodowa - 1967	6378160.000	6356774.719	298.250	0.00669454	AND
8	Airy 1830.	6377563.396		299.325
9	Modified Airy	6377340.189		299.325
10	Australian National	6378160.000		298.250
11	Bessel 1841 (Namibia)	6377483.865		299.153
12	Bessel 1841	6377397.155		299.153
13	Clarke 1866.	6378206.400		294.979
14	Clarke 1880.	6378249.145		293.465
15	Everest (Sabah Sarawak)	6377298.556		300.802
16	Everest (India 1956)	6377301.243		300.802
17	Everest (Malaysia 1969)	6377295.664		300.802
18	Everest (Malay. & Sing)	6377304.063		300.802
19	Everest (Pakistan)	6377309.613		300.802
20	Modified Fischer 1960	6378155.000		298.300
21	Helmert 1906	6378200.000		298.300
22	Hough 1960	6378270.000		297.000
23	Indonesian 1974	6378160.000		298.247
24	Hayford 1924	6378388.000		297.000
25	GRS 80	6378137.000		298.257
26	South American 1969	6378160.000		298.250
27	WGS - 72	6378135.000	6356750.520	298.260	0.00669432	WGS-72
28	WGS – 84	6378137.000	6356752.3142	298.257	0.00669438	WGS-84

Góra strony

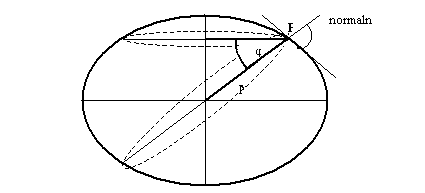
1.2. Przekroje główne elipsoidy

W każdym punkcie P powierzchni elipsoidy można poprowadzić prostą n prostopadłą (normalną) do powierzchni. Nieskończenie wiele płaszczyzn zawierających normalną n przecina powierzchnię elipsoidy w nieskończenie wielu krzywych zbiegających się w punkcie P.

Płaszczyzny, które zawierają w danym punkcie normalną n, która jest prostopadła do elipsoidy nazywamy płaszczyznami normalnymi.

Natomiast przekrojami tej normalnej są krzywe uzyskane na powierzchni elipsoidy w wyniku przecięcia jej płaszczyznami normalnymi, zawierającymi normalną, w danym punkcie do elipsoidy. Wśród nieskończenie wielu przekrojów normalnych elipsoidy wyróżnia się dwa przekroje główne, których płaszczyzny normalne tworzą z sobą kąt prosty, a z otrzymanych krzywych na powierzchni elipsoidy jedna ma krzywiznę największą a, druga zaś najmniejszą w punkcie P. Jednym z przekrojów głównych jest przekrój prostopadły do południka, zwany pierwszym wertykałem lub przekrojem poprzecznym, a drugim przekrój południkowy – krzywa uzyskana na powierzchni elipsoidy w wyniku przecięcia jej płaszczyzną południkową.

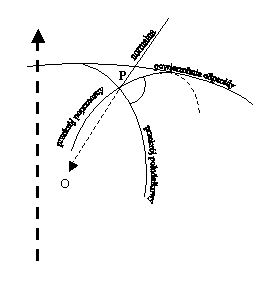
Rys. 4. Przekroje główne elipsoidy w punkcie

Promień krzywizny przekroju południkowego jest najmniejszy, a więc krzywizna jest największa. Natomiast promień krzywizny pierwszego wertykału jest największy, więc krzywizna jest najmniejsza.

Przekroje normalne zawarte pomiędzy przekrojami głównymi mają krzywizny i promienie pośrednie. Są to przekroje normalne dowolne.

Promień krzywizny przekroju południkowego M wyrażony jest następującym wzorem:

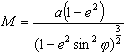
Promień równoleżnika z twierdzenia Meusniera: promień równoleżnika jest równy iloczynowi promienia krzywizny tego przekroju poprzecznego i cosinusa szerokości, jeżeli płaszczyzna przekroju poprzecznego i płaszczyzna równoleżnika tworzą ze sobą kąt równy szerokości geodezyjnej i mają wspólną styczną do równoleżnika w punkcie P

Rys. 5. Promień krzywizny przekroju południka

r= Ncosφ

Promień równoleżnika można wyliczyć w funkcji szerokości

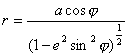
stąd:

promień krzywizny przekroju poprzecznego N wyrażamy zależnością:

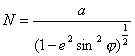
W obu biegunach promień krzywizny wszystkich przekrojów normalnych są sobie równe i wynoszą:

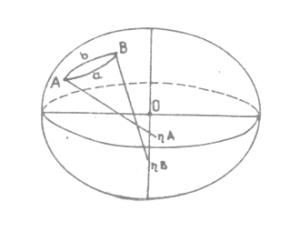
Rys. 6. Wzajemne przekroje normalne w punktach A i B na powierzchni elipsoidy.

Przekrojem normalnym elipsoidy w punkcie A nazywa się taki przekrój, którego płaszczyzna przechodzi przez normalną do punktu A. Jeżeli na powierzchni elipsoidy występują dwa punkty: A oraz B, to ich wzajemne przekroje normalne nie pokrywają się.

Płaszczyzna przekroju normalnego w punkcie A przechodzi zwykle przez normalną punktu A oraz przez punkt B, ale płaszczyzna ta nie zawiera na ogół normalnej do płaszczyzny w punkcie B z wyjątkiem przypadku, gdy punkty te leżą na wspólnym południku lub równoleżniku.

Wzajemne przekroje normalne są względem siebie „wichrowate”. Przekrój wprost w punkcie A, tj. łuk AaB nie pokrywa się z przekrojem odwrotnym w tym punkcie, mianowicie z łukiem BbA.

Kąt między wzajemnymi przekrojami normalnymi można obliczyć według następującej zależności:

gdzie:

s – odległość między punktami,

- wartość radiana wyrażona w sekundach,

- średni promień Ziemi.

Promień krzywizny przekroju normalnego można obliczyć z zależności:

gdzie:

-azymut przekroju normalnego,

Góra strony

1.3. Linia geodezyjna

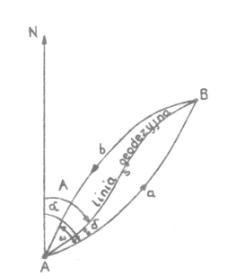
Rys. 7 Przebieg linii geodezyjnej i przekrojów normalnych między dwoma punktami.

Linia geodezyjna na danej powierzchni to taka krzywa, której płaszczyzna, ściśle styczna w każdym jej punkcie, przechodzi przez normalną do powierzchni w tym punkcie. Jest ona jednocześnie najkrótszą odległością między dwoma punktami na powierzchni elipsoidy obrotowej. Ze względu na to taką linię geodezyjną określa się jako ortodromę na powierzchni elipsoidy obrotowej.

Płaszczyznę ściśle styczną do pewnej powierzchni stanowi płaszczyzna, która przechodzi przez styczną do krzywej jak i przez inny punkt na niej, leżący nieskończenie blisko punktu styczności.

Na (rysunku 1.4.) zaprezentowano przebieg linii geodezyjnej między punktami A i B oraz jej położenie w stosunku do przekrojów normalnych, tj.:

- wprost krzywa AaB,

- odwrotnie krzywa BbA.

Linia geodezyjna na powierzchni elipsoidy ( przy azymutach nie zbliżonych do i ) dzieli kąt między wzajemnymi przekrojami normalnymi w przybliżeniu w stosunku 1:2 i położona jest w danym punkcie bliżej przekroju normalnego wprost. Kąt zawarty między linią geodezyjną łączącą punkty A i B a przekrojem normalnym wprost w każdym z tych punktów ( ), równy jest 1/3 kąta zawartego między przekrojem normalnym wprost a przekrojem odwrotnym w danym punkcie, tj.:

gdzie:

- kąt zawarty między przekrojem normalnym wprost a przekrojem odwrotnym w danym punkcie,

- kąt zawarty między linią geodezyjną a przekrojem normalnym wprost.

Wartość kąta można obliczyć według wzoru:

gdzie:

s – odległość między punktami,

- wartość radiana wyrażona w sekundach,

- średni promień Ziemi,

- azymut przekroju normalnego,

e – pierwszy mimośród elipsoidy.

Linia geodezyjna jest najkrótszą odległością pomiędzy dwoma punktami na powierzchni elipsoidy. Jej długość jest na pewno krótsza niż długość łuku przekroju normalnego. W praktyce jednak długość przekroju normalnego i linii geodezyjnej jest wartością bardzo małą i z reguły pomija się nawet w bardzo dokładnych obliczeniach.

Różniczkę łuku linii geodezyjnej przedstawiamy zależnością:

Ds = ,

gdzie:

Ds – różniczka łuku linii geodezyjnej,

M – promień krzywizny południka,

N – promień krzywizny pierwszego wertykału,

- szerokość geograficzna,

- długość geograficzna.

Natomiast długość linii geodezyjnej określa następujące równanie:

S =,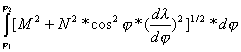

gdzie:

S – długość linii geodezyjnej.

Twierdzenie Clairauta polegające na ukazaniu możliwości wyznaczenia spłaszczenia geometrycznego f za pomocą wielkości czysto dynamicznych: przyśpieszeń sił ciężkości określających f oraz parametru q zależnego od prędkości wirowania Ziemi , wymiaru elipsoidy b lub a i masy Ziemi, ważne jest dla dowolnej powierzchni obrotowej:

R = a cos u,

gdzie:

R – promień Ziemi,

a – duża półoś elipsoidy,

u – szerokość zredukowana.

Dlatego też równanie powyższe można napisać w postaci;

a*cos u*sinA = const.

Z wyrażenia a*cos u*sinA = const wynika, że dla linii geodezyjnej na powierzchni elipsoidy obrotowej iloczyn cosinusa szerokości zredukowanej punktu linii geodezyjnej i sinusa jej azymutu jest wielkością stałą, to znaczy:

Zależność ta pozwala na ogólną analizę przebiegu ortodromy na powierzchni elipsoidy obrotowej. W punkcie W (rys.5.) ortodroma osiąga największą szerokość zredukowaną (i geograficzną). Punkt ten nazywa się wierzchołkiem ortodromy (linii geodezyjnej). W tym punkcie azymut linii geodezyjnej jest równy.

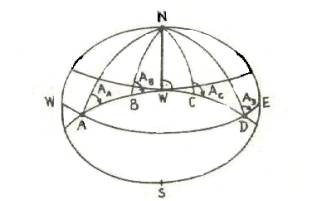
Rys. 8 Przebieg linii geodezyjnej na powierzchni elipsoidy obrotowej.

Góra strony

1.4. Długość łuku południka.

Długość łuku południka między punktami o szerokościach wyraża się wzorem:

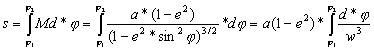, [1]

gdzie:

s – długość łuku południka,

M – promień krzywizny południka,

a – duża półoś elipsoidy,

e – pierwszy mimośród elipsoidy,

- szerokość geograficzna.

Całka ta nie daje się rozwiązać w postaci elementarnej. Dlatego też funkcję podcałkową należy rozwinąć w szereg Newtona, a następnie przeprowadzić całkowanie poszczególnych wyrazów.

Ograniczając się do wyrazów zawierających e⁶, rozwinięcie w szereg daje:

Parzyste potęgi sinusów wchodzących w rozwinięcie zamienia się na cosinusy parzystych łuków, zgodnie z równościami:

Wyrażenie

można więc przedstawić w postaci:

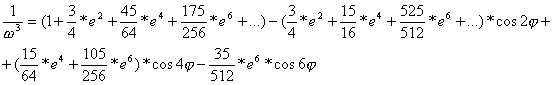
Wprowadzając oznaczenia:

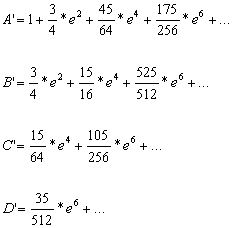
i wstawiając je do wzoru [1] otrzymamy:

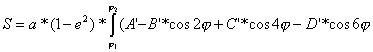Po przeprowadzeniu całkowania otrzymamy:

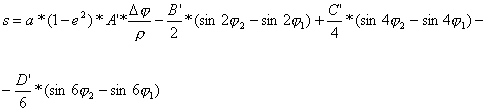[2]

gdzie:

wartość jednego radiana wyrażona w tych samych jednostkach co i .

Wprowadza się oznaczenia:

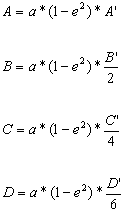[3]

Zależność [2] służąca do obliczania długości łuku południka, z uwzględnieniem oznaczeń [3], przyjmuje postać:

[4]

gdzie:

s - długość łuku południka,

- szerokość geograficzna,

wartość jednego radiana wyrażona w tych samych jednostkach co i .

Jeżeli długość łuku południka liczy się od równika (), to wyrażenie [4] przyjmie postać:

Góra strony

1.5. Długość łuku równoleżnika.

Równoleżnik na elipsoidzie obrotowej jest okręgiem koła. Promień równoleżnika r, zgodnie z wzorami:

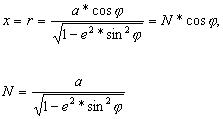
wynosi:

gdzie:

r – promień równoleżnika,

a – duża półoś elipsoidy,

e – pierwszy mimośród elipsoidy,

N – promień krzywizny pierwszego wertykału.

Obecnie istnieje wiele elipsoid odniesienia oraz układów odniesienia. To ostatnie pojęcie jest znacznie szersze od poprzedniego, gdyż obejmuje zarówno samą elipsoidę odniesienia ( jej wymiary), jak i jej zorientowanie (punkt przyłożenia i zorientowanie w bryle geoidy).

Góra strony

2. Układy odniesienia i ich opis

Układ współrzędnych jest pojęciem matematycznym, abstrakcyjnym, a więc nie związanym z fizyczną powierzchnią ziemi. Wynika z tego, że posługując się tak samo brzmiącymi nazwami układów współrzędnych możemy określić różne wartości współrzędnych tego samego punktu. Spowodowane to jest tym, że układy te mogą być względem siebie przesunięte i obrócone. Wynika stąd wniosek, że mówiąc o konkretnym układzie współrzędnych należałoby go związać z określonym ciałem fizycznym. Powoduje to potrzebę wprowadzenia pojęcia układu odniesienia.

Układ odniesienia to konkretny układ współrzędnych, w ścisły sposób związany z ciałem lub układem ciał fizycznych.

W praktyce powiązanie to realizowane jest poprzez określenie współrzędnych pewnego fizycznego punktu lub kilku punktów związanych z Ziemią (np. wybrany punkt na powierzchni Ziemi) oraz orientacji układu współrzędnych.

W drugiej połowie lat osiemdziesiątych w różnych państwach świata stosowano różne układy odniesienia (niekiedy nawet na terenie jednego państwa). Doszło nawet i do tego, że wydawane przez daną instytucję mapy nawigacyjne określonego rejonu opracowane były w zależności od skali w różnych układach odniesienia. Sytuacja taka miała miejsce na przykład w wypadku map Cieśniny Dover wydawanych przez Admiralicję Brytyjską, gdyż dla jednych z nich układem odniesienia był układ Urzędu Pomiarowego Wielkiej Brytanii z 1936 roku, zaś dla innych układ europejski ED-50.

Obecnie stosowanych jest jeszcze wiele układów odniesienia. Chociaż występują już tendencje do ich ujednolicania i przyjęcia jednego, wspólnego globalnego układu odniesienia dla potrzeb geodezji i nawigacji. Problem jest złożony i możliwy do realizacji dopiero współcześnie. Stało się to dzięki rozwojowi geodezji i nawigacji satelitarnej. Zadanie utworzenia układu odniesienia sprowadza się do wyboru układu współrzędnych, jego odpowiedniej orientacji i powiązania z fizyczną bryłą Ziemi. Obecnie w geodezji i nawigacji najczęściej stosowanym układem współrzędnych jest układ współrzędnych geodezyjnych na elipsoidzie. Należy przy tym zauważyć, że konkretna elipsoida odniesienia ma ściśle określone położenie i orientację względem bryły Ziemi.

Określenie układu odniesienia pozwala na prowadzenie w nim pomiarów współrzędnych dowolnych punktów. Istniejąca obecnie duża ilość układów odniesienia wynika z dwóch zasadniczych przyczyn. Najistotniejszą było prowadzenie w przeszłości, w poszczególnych państwach, nieskoordynowanych wzajemnie prac badawczych, mających na celu utworzenie lokalnych układów odniesienia. Nie mniej istotne są też względy wojskowe, mające na celu utrudnienie potencjalnemu przeciwnikowi przygotowanie szczegółowych map cudzego terytorium. Przy współczesnym rozwoju techniki, szczególnie satelitarnej, ta druga przyczyna zaczęła tracić na znaczeniu. Zwłaszcza, że stosowanie globalnych i dokładnych systemów nawigacyjnych wymaga poprawnego określenia światowego układu odniesienia. Jednakże układy lokalne i regionalne nie tracą przy tym całkowicie swojego znaczenia.

Góra strony

2.1. Charakterystyka lokalnych układów odniesienia.

Zostały stworzone celem jak najwierniejszego odwzorowania wybranego fragmentu powierzchni Ziemi: rejon geograficzny, kontynent, teren danego państwa itp. Są to układy, w których parametry przyjętej elipsoidy odniesienia zostały wyznaczone najczęściej na podstawie pomiarów naziemnych, a zorientowanie owej elipsoidy względem geoidy polegało na takim określeniu punktu przyłożenia, aby powierzchnia elipsoidy, na objętym danym układem fragmencie powierzchni Ziemi, była jak najbardziej zbliżona do powierzchni geoidy. Lokalne układy odniesienia są układami quasi-geocentrycznymi, w których początek znajduje się w środku przyjętej elipsoidy odniesienia. Do układów tych zaliczamy:

Góra strony

2.2.1.Układ północnoamerykański (NAD 27).

Układ ten jest stosowany na kontynencie północnoamerykańskim od Alaski po Meksyk i Amerykę Środkową z Wyspami Karaibskimi i Grenlandią. Oparty jest on o elipsoidę Clarke’a z 1866 roku zorientowaną wielopunktowo z punktem przyłożenia w Neades Ranch w stanie Kansas.

Góra strony

2.2.2 Układ europejski (ED 50).

Układ ten obejmuje część Europy, Afryki i Azji. Oparty jest o elipsoidę Hayforda z punktem przyłożenia w Poczdamie i zorientowaną wielopunktowo.

2.2.3 Układ indyjski (IND).

Obejmuje on terytorium Indii oraz państw sąsiednich. Utworzony w oparciu o elipsoidę Everesta z punktem przyłożenia w Kalianpur (Środkowe Indie). Elipsoida ta pochodzi z 1830 roku i jest jedna z najstarszych obecnie stosowanych elipsoid.

2.2.4 Układ japoński (JAP).

Oparty jest o elipsoidę Bessela z punktem przyłożenia w starym tokijskim obserwatorium astronomicznym. Zasięgiem swoim obejmuje Japonię oraz poprzez sieć triangulacyjną także terytorium Korei i sięga aż po Mandzurię.

2.2.5 Układ ‘42’ (URSS).

Obejmuje terytorium Rosji oraz sąsiednich państw byłego Związku Radzieckiego. Oparty jest o elipsoidę Krasowskiego, która została opracowana na podstawie obszernych badań obejmujących swoim zasięgiem znaczne obszary Europy, Azji oraz Ameryki Północnej. Dzięki temu jest ona jedna z najbliższych geoidzie elipsoid klasycznych. Zorientowano ją wielopunktowo z punktem przyłożenia w obserwatorium w Pułkowie koło Leningradu.

2.2.6 Układ południowoamerykański (SAD).

Oparty jest o elipsoidę Hayforda z punktem przyłożenia w La Canoa w Wenezueli. Swoim zasięgiem obejmuje tereny Ameryki Południowej.

2.2.7 Układ afrykański (ARC).

Obejmuje on obszar całej Afryki. Oparty jest o elipsoidę Clarke’a (1880r.) z punktem przyłożenia znajdującym się w Cape of Good Hope (Buffalafontein).

2.2.8 Układ australijski (AND).

Układ oparty jest o elipsoidę Nowa A.I.G. (1967r.) z punktem przyłożenia umieszczonym w Johnstown. Obejmuje on tereny Afryki.

2.2.9 Układ argentyński (ARG).

Obejmuje tereny Argentyny. Oparty jest o elipsoidę Hayforda (1909r.), zorientowaną wielopunktowo z punktem przyłożenia w Campo Inchauste.

2.2.10 Układ Hawajski (HAW).

Układ ten swoim zasięgiem obejmuje tereny hawajskie. Oparty jest o elipsoidę Clarke’a (1866r.), zorientowaną wielopunktowo z punktem przyłożenia znajdującym się w Diamand Head.

Góra strony

2.2. Charakterystyka układów geocentrycznych.

Układy geocentryczne (globalne), stworzone celem jak najwierniejszego odwzorowania całej powierzchni Ziemi. Są to układy, w których parametry elipsoidy odniesienia zostały wyznaczone na podstawie pomiarów naziemnych (geodezyjnych, astronomicznych, grawimetrycznych) oraz wyników obserwacji sztucznych satelitów Ziemi, a zorientowanie elipsoidy względem geoidy polegało na takim określeniu punktu przyłożenia, by powierzchnia elipsoidy na całej powierzchni Ziemi była jak najbardziej zbliżona do powierzchni geoidy. Globalne układy odniesienia są układami geocentrycznymi, których początek znajduje się w środku masy Ziemi.

Rozwój geodezji satelitarnej oraz satelitarnych systemów nawigacyjnych stworzył potrzebę, a jednocześnie realną możliwość, opracowania światowego układu odniesienia. Pierwszym globalnym układem, w którym wykorzystano pomiary satelitarne, był WGS 60 (World Geodetic System). Potem kolejno opracowano: w 1967 roku WGS 66 i w 1975 roku – WGS 72. Natomiast od 1987 roku zaczęto wykorzystywać układ WGS 84. Równolegle stosowany jest także satelitarny układ odniesienia NWL 9D. Jednakże nie jest on wykorzystywany w nawigacji.

Wszystkie te globalne układy odniesienia obejmują swym zasięgiem obszar całego świata. Elipsoidą odniesienia jest elipsoida ziemska, natomiast punkt przyłożenia stanowi środek geoidy.