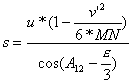OBLICZANIE WSPÓŁRZEDNYCH NA POWIERZCHNI ELIPSOIDY OBROTOWEJ

Opis metod przenoszenia współrzędnych. 1

1. Metody wykorzystujące punkt pomocniczy. 1

1.1. Metoda Clarke’a (zadanie wprost) 2

1.2. Metoda Clarke’a (zadanie odwrotne). 8

1.3. Metoda Schreibera. 11

2. Metody wykorzystujące szeregi potęgowe Legendre’a. 14

2.1. Metoda średniej szerokości Gaussa - zadanie wprost 14

2.2. Metoda średniej szerokości Gaussa zadanie odwrotne. 36

3. Metody bezpośrednie. 55

3.1. Metoda Bessela zadanie wprost 76

3.2. Metoda Bessela zadanie odwrotne. 149

4. Metody wykorzystujące cięciwy elipsoidy. 194

4.1. Metoda Mołodeńskiego. 197

Bibliografia: 249

Opis metod przenoszenia współrzędnych

Klasyczny problem obliczania współrzędnych geodezyjnych na powierzchni elipsoidy obrotowej oraz azymutów i długości linii geodezyjnych nosi nazwę przenoszenia współrzędnych. Wyróżniamy dwa rodzaje problemu: tzw. zadanie wprost i zadanie odwrotne.

Zadanie pierwsze zwane zadaniem wprost dotyczy obliczenia współrzędnych geodezyjnych B₂, L₂ punktu P₂ i azymutu (odwrotnego) A₂₁ linii geodezyjnej, gdy znane są współrzędne geodezyjne B₁, L₁ punktu P₁, długość linii geodezyjnej s₁₂ oraz azymut (wprost) A₁₂, pod jakim linia geodezyjna wychodzi z punktu P₁.

Zadanie drugie zwane zadaniem odwrotnym dotyczy obliczenia długości linii geodezyjnej s₁₂ łączącej na powierzchni elipsoidy dwa punkty o znanych współrzędnych P₁ (B₁, L₁) i P₂ (B₂, L₂) oraz obliczenia azymutów linii geodezyjnej (wprost i odwrotnego) A₁₂ i A₂₁.

Z powodu wysokich wymagań dokładności a także trudności bezpośredniego rozwiązywania zadań związanych z przenoszeniem współrzędnych na powierzchni elipsoidy ziemskiej, geodezja wyższa staje się ważnym elementem związanym z nawigacją. Wymagania te polegają na opracowaniu wzorów zapewniających pewną dokładność obliczeń, przy odpowiednim stopniu ich skomplikowania w zależności od sprzętu, którym dysponuje liczący. Stworzono wiele algorytmów i różnych pomocy rachunkowych. W obecnych latach, z uwagi na automatyzację obliczeń, wiele wcześniej dostępnych metod obliczania współrzędnych utraciło swoje dawne znaczenie. Powstały i ciągle powstają nowe metody.

Najogólniej metody klasyczne obliczania współrzędnych dzielimy na cztery grupy:

• Metody wykorzystujące punkt pomocniczy.
• Metody wykorzystujące szeregi potęgowe Legendre’a.
• Metody bezpośrednie.
• Metody wykorzystujące cięciwy elipsoidy.

1. Metody wykorzystujące punkt pomocniczy.

Kiedy odległość pomiędzy punktami początkowym i końcowym linii geodezyjnej s jest rzędu kilkudziesięciu kilometrów to trójkąt geodezyjny P₁P₂B jest bardzo smukły (rys.1.), ponieważ dwa jego boki łączące punkty linii geodezyjnej z biegunem mogą osiągać znaczne długości. Niekorzystne byłoby z uwagi na dokładność obliczeń stosowanie bezpośrednich metod rozwiązywania takiego trójkąta.

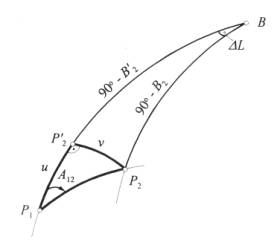
Rys. 1. Metoda punktu pomocniczego

Kiedy prowadzimy przekrój normalny przez punkt P₂ prostopadły do południka punktu P₁ otrzymujemy mały prostokątny trójkąt P₁P₂^’ P₂, który rozwiązuje się na sferze o promieniu R_s1. Wyznaczenie boku u tego trójkąta pozwala na wyliczenie szerokości punktu P₂’, którą można traktować jako przybliżenie poszukiwanej szerokości punktu P₂. Poprawkę do takiej przybliżonej szerokości można dostatecznie dokładnie wyznaczyć z trójkąta P₂’BP₂. Dla wyznaczenia i budujemy pewien sferyczny trójkąt biegunowy.

Metoda punktu pomocniczego w wersji Clarke’a służy zazwyczaj do rozwiązywania zadania wprost dla odległości do 30 kilometrów. W wersji Schreibera, połączona z szeregami potęgowymi, nadaje się do odległości 60 km a nawet 120 km w zależności od rzędu wyrazów (różniczek) wykorzystanych w szeregach potęgowych (trzeci lub czwarty rząd).

1.1. Metoda Clarke’a (zadanie wprost)

Rys. 2. Trójkąt sferoidalny.

Rys. 3 Trójkąt płaski

Na elipsoidzie o parametrach a i e dany jest punkt P₁ (rys.2.) o współrzędnych B₁ i L₁, znamy również odległość geodezyjna s = P₁P₂ oraz azymut A₁₂. Obliczyć mamy współrzędne B₂, L₂ punktu P₂ oraz azymut A₂₁ (azymut odwrotny).

Kiedy z punktu P₂ poprowadzimy ortodromę (linię geodezyjną) prostopadłą do południka P₁P_N wtedy punkt P₂ będzie stanowił punkt przecięcia ortodromy z południkiem P₁P_N. Z powodu tego, że boki trójkąta P₁P₂P₂’ są małe, to zgodnie z twierdzeniem Bessela, trójkąt ten można uważać za trójkąt sferyczny na kuli o promieniu . W wyniku tego otrzymujemy trójkąt sferyczny o elementach:

A₁₂, , u, v, s oraz .

Nadmiar sferyczny obliczamy ze wzoru:

gdzie:

- nadmiar sferyczny,

R – promień kuli,

P – powierzchnia trójkąta płaskiego o elementach A₁₂, s, ,

P = ,

,

,

- wartość jednego radiana wyrażona w sekundach kątowych.

Jeśli pozbędziemy się drugiego członu otrzymamy, że:

,

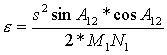gdzie:

s – długość linii geodezyjnej,

A₁₂- azymut wprost,

M,N – główne promienie krzywizny.

W trójkącie sferycznym P₁P₂P₂’ możemy określić kąt

.

„Twierdzenie Legendre’a mówi, że mały trójkąt sferyczny można rozwiązać zamieniając go na trójkąt płaski, w którym długości boków pozostają niezmienione w stosunku do odpowiednich długości na sferze, każdy kąt zaś jest zmniejszony o nadmiaru sferycznego.”

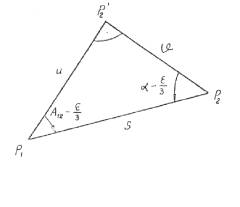
W wyniku użycia twierdzenia Legendre’a dla małych trójkątów rozwiązujemy trójkąt płaski u, v, s, którego kąty są równe:

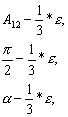
przy czym

.

Jeśli zastosujemy wzory sinusowe trygonometrii płaskiej uzyskamy wtedy elementy małego trójkąta sferycznego:

,

,

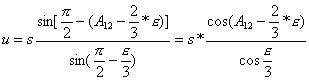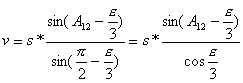gdzie:

s – długość linii geodezyjnej,

A₁₂- azymut wprost,

- nadmiar sferyczny,

- wartość stała.

Wiemy, że przyjmuje wartość małego kąta dlatego zakładamy

.

Kontynuując otrzymujemy:

,

.

Wykorzystując obliczoną wartość u obliczymy B₂’, a następnie B₂. W tym celu obliczymy najpierw wielkość jako kąt środkowy odpowiadający łukowi kołowemu u o promieniu M₁. Następnie obliczamy przybliżoną wartość szerokości geodezyjnej B_s dla punktu P_s pośredniego między P₁ i P₂’ czyli:

,

gdzie:

B_s – przybliżona wartość szerokości geodezyjnej punktu P_s,

B₁ – szerokość geodezyjna dla P₁,

B₀ – kąt odpowiadający łukowi kołowemu u o promieniu M₁.

Można teraz obliczyć M_s dla punktu P_s. Ponieważ u jest łukiem południka między punktami P₁ i P₂’, to

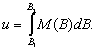
Kiedy przyjmiemy, że M(B) = M_s w przedziale [B₁, B₂’] otrzymamy

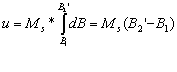
gdzie:

M_s – promień krzywizny w punkcie P_s,

B₂ – szerokość geodezyjna punktu P₂,

B₁ – szerokość geodezyjna dla P₁.

Wobec tego

,

.

Według autora w następnej kolejności powinniśmy obliczyć różnicę B₂’ – B₂. Uwzględniając to, że v jest wielkością małą w stosunku do promienia kuli R, trójkąt P₂P_nP₂’ możemy rozwiązać jako prostokątny trójkąt sferyczny. Mamy więc:

czyli

,

skąd

,

więc

,

gdzie:

,

.

Z tego względu, że bok v jest mały, boki niewiele się od siebie różnią i różnica jest małym kątem. Możemy zatem przyjąć:

czyli

,

.

Otrzymamy wtedy

i

.

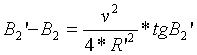Szerokość geodezyjna punktu P₂ będzie równa:

.

Należy jeszcze wyprowadzić wzór na różnicę długości geodezyjnej

.

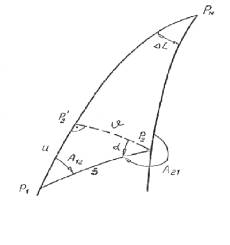
W tym celu skorzystamy z pomocniczej kuli o promieniu . W punkcie P₂ prostopadle do łuku P₂P₂’ (rys.4.) poprowadzimy ortodromę P₂T. Punkt T przecięcia się ortodromy z południkiem P₂’P_N jest biegunem łuku P₂P₂’ (uważanego za łuk koła wielkiego), więc

.

Zatem w trójkącie P₂BT jest

, kąt , kąt .

Kąt przy P₂ oznaczamy przez . Jest to zbieżność (konwergencja) południków punktu P₁ i punktu P₂. Tym sposobem otrzymujemy jeszcze jeden trójkąt P₂P_sT, którego boki są równe:

, , ,

natomiast kąty są równe:

, , .

W otrzymanym trójkącie występują pewne elementy oraz kat związany z azymutem A₂₁. W celu rozwiązania trójkąta sferycznego P₂P_sT konstruujemy odpowiadający jemu trójkąt biegunowy pnt (rys. 4.). Według twierdzenia mówiącego, że boki i kąty odpowiednie obu trójkątów dopełniają się do 180°, otrzymamy następujące elementy trójkąta biegunowego:

Kąty , , ,

Boki , , .

Otrzymaliśmy w ten sposób trójkąt sferyczny o małych bokach, który możemy rozwiązać metodą Legendre’a. W tym celu musimy znać jego nadwyżkę sferyczną .

Będziemy mieli:

,

gdzie:

- nadwyżka sferyczna,

B –szerokość geodezyjna.

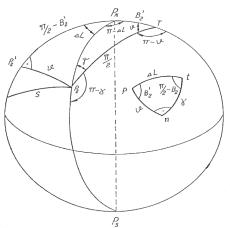
Rys. 4 Kula pomocnicza w metodzie Clarke’a.

Wartość tę już wcześniej obliczyliśmy. Zatem trójkątem płaskim, który mamy rozwiązać jest trójkąt o bokach i , kątach:

, , .

Korzystamy z twierdzenia sinusów i otrzymujemy:

,

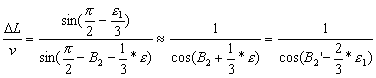gdzie:

v –długość boku pn (rys. 4.),

- nadwyżka sferyczna

B –szerokość geodezyjna,

- różnica długości geodezyjnej.

Należy pamiętać o założeniu, że . Ponieważ , to

.

Mamy więc

lub

.

Krótki łuk ortodromy możemy zastąpić łukiem przekroju normalnego poprzecznego w punkcie P₂’, więc przechodząc na miarę kątową za pomocą promienia N’ (dla szerokości B₂’) otrzymamy:

,

gdzie:

N’ – promień krzywizny.

Aby uzyskać zbieżność południków zastosujemy twierdzenie sinusów w postaci:

,

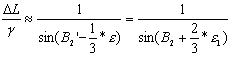gdzie:

- zbieżność południków

Stąd zbieżność południków będzie równa:

.

Natomiast azymut odwrotny będzie równy:

,

czyli

,

przy czym znak zależny jest od wzajemnego usytuowania punktów P₁ i P₂.

„Zadanie wprost w rzeczywistości rozwiązane na kulach pomocniczych, ale na mocy twierdzenia Bessela dla długości mniejszych od 50 km, wyniki pozostają ważne także dla elipsoidy”.

Ostateczne rozwiązanie:

,

,

.

Góra strony

1.2. Metoda Clarke’a (zadanie odwrotne).

W zadaniach tego typu dane mamy na elipsoidzie punkty P₁ (B₁, L₁) i P₂ (B₂, L₂). Znamy więc i . Szukamy natomiast azymutów A₁₂, A₂₁ oraz długości ortodromy s. Podobnie jak w zadaniu wprost wykorzystamy rozważania i obliczenia wykonane na kuli pomocniczej. Pomocniczy bok trójkąta obliczymy przekształcając równanie:

,

wówczas otrzymamy

gdzie:

v – kąt środkowy

Z powodu tego, że jest nieznane, obliczymy je za pomocą kolejnych przybliżeń. Na początku kroku przyjmijmy , to:

,

gdzie:

v – kąt środkowy.

Uwzględniając [5] oraz [6] mamy

,

gdzie:

v – długość łuku (wymiar liniowy)

Możemy więc obecnie napisać:

.

Podstawiając otrzymamy

.

Wracając do równania [7] i po przekształceniach otrzymamy następne przybliżenie:

. [8]

Wobec tego jako drugie i już wystarczająco dokładne przybliżenie dla mamy:

,

gdzie:

v – obliczamy ze wzoru [8].

Mamy więc

i szerokość średnia

.

Obliczamy następnie długość łuków v’ i u (jako łuków kołowych)

lub ,

oraz

,

gdzie:

v’, u – długości łuków (kołowych),

M, N – główne promienie krzywizny,

B₁, B₂ – szerokości geodezyjne.

Korzystając z tego, że:

,

mamy:

. [9]

Z równań:

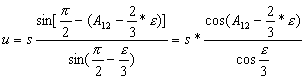, [10]

,

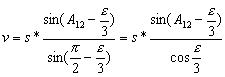gdzie:

s – długość linii geodezyjnej,

A₁₂- azymut wprost,

- nadmiar sferyczny,

- wartość stała,

wyliczymy:

,

.

Zakładając, że i , będziemy mieli:

,

skąd

.

Uwzględniając [9] mamy:

,

gdzie:

s – długość linii geodezyjnej,

A₁₂ – azymut wprost,

- nadmiar sferyczny,

M, N – główne promienie krzywizny,

v’, u – długości łuków.

W dalszym ciągu będziemy mieli:

,

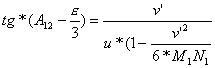czyli

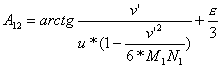
Azymut odwrotny A₂₁ obliczymy ze wzoru:

,

gdzie jest obliczona za pomocą wzoru:

.

Długość łuku ortodromy obliczymy według wzoru:

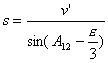
lub wzoru

.

Ostateczne rozwiązanie zadania to:

,

Góra strony

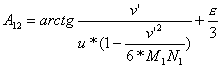
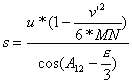
1.3. Metoda Schreibera.

Metoda Schreibera polega na rozwinięciu różnic współrzędnych i azymutu na szeregi według potęg długości s ortodromy dla punktu początkowego i końcowego, przy czym uwzględnione zostają wielkości małe, czwartego rzędu. Zadanie to rozwiązywać można dla odległości mniejszych od 150 km oraz do szerokości geodezyjnych niezbyt bliskich

biegunów. Służy ona do rozwiązywania zadania wprost.

Zajmujemy się rozwiązaniem trójkąta elipsoidalnego, biegunowego P₁P₂P_N (rys.5. ). Współrzędne geodezyjne B₁, L₁, azymut A₁₂ ortodromy w punkcie P₁ oraz długość ortodromy s są znane.

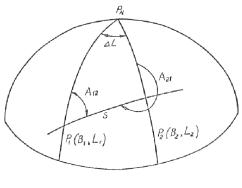
Rys. 5 Trójkąt elipsoidalny w metodzie Schreibera.

Szukamy współrzędnych punktu P₂ (B₂, L₂) i azymut odwrotny A₂₁. Zadanie polega na rozwiązaniu trójkąta elipsoidalnego skonstruowanego w następujący sposób: z punktu P₂ prowadzimy ortodromę prostopadłą do południka punktu P₁, która przecina ten południk w punkcie P₂’ (podobnie jak w metodzie Clarke’a). Otrzymujemy w ten sposób mały trójkąt elipsoidalny P₁P₂P₂’, który możemy z dokładnością do wielkości małych rzędu e²*s*R³, uważać za prostokątny trójkąt sferyczny o takich samych bokach s, v, u. Promień kuli pomocniczej jest równy średniemu promieniowi krzywizny elipsoidy w punkcie P₁, tj. .

Tak wyznaczony trójkąt sferyczny ma takie same boki jak i odpowiadający mu trójkąt elipsoidalny. Nadmiary sumy kątów są sobie równe z dokładnością do e²*s*R³. Ze wzoru:

, [11]

obliczymy nadmiar sferyczny. Znając w trójkącie sferycznym, a tym samym w trójkącie elipsoidalnym, możemy określić kąt sferyczny , mianowicie:

.

Obecnie możemy rozwiązać trójkąt sferyczny stosując metodę Legendre’a, tj. rozwiązać go jako trójkąt płaski o następujących kątach;

, i .

Z twierdzenia sinusów trygonometrii płaskiej, otrzymamy boki u i v trójkąta sferycznego (a tym samym elipsoidalnego). Z powodu tego, że jest kątem małym rzędu s*N², możemy więc w przybliżeniu przyjąć . Korzystamy przy tym oczywiście z wcześniej otrzymanych równań [10.]

Wobec tego będziemy mieli:

,

.

Po rozwinięciu i uwzględnieniu, że:

oraz i

otrzymamy:

,

.

Gdy wprowadzimy oznaczenia Schreibera x = s*cos A₁₂ oraz y = s*sin A₁₂ i uwzględnimy [11] otrzymamy:

.

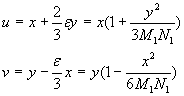Według autora Schreiber na podstawie rozwinięcia szeregów potęgowych na przenoszenie współrzędnych wyprowadził wzory na różnice szerokości i długości geodezyjnej. Różnica szerokości geodezyjnej pomiędzy punktami P₁ i P₂ jest równa:

, [12]

gdzie:

x = scos A_12,

y = ssin A₁₂,

,

M₁, N₁ –główne promienie krzywizny,

B’- różnica szerokości geodezyjnej pomiędzy punktami P₁ i P_2,

B₁, B₂ – szerokości geodezyjne,

a – duża półoś elipsoidy,

e – pierwszy mimośród elipsoidy.

Różnica długości zaś, pomiędzy punktami P₂’ i P₂ (ponieważ punkty P₁ i P₂’ leżą na tym samym południku, to ten sam wzór wyraża różnicę długości pomiędzy P₁ i P₂) określamy wzorem:

gdzie:

N’- przekrój poprzeczny w punkcie B₂’.

Natomiast różnica szerokości geodezyjnej pomiędzy punktami P₂’ i P₂ wyraża się wzorem:

, [13]

Odejmując stronami od wzoru [12] wzór [13] otrzymamy wyrażenie na szukaną różnicę szerokości geodezyjnej punktów P₁ i P₂. Mamy:

,

stąd

.

Azymut odwrotny A₂₁ obliczymy z zależności :

,

gdzie:

- zbieżność południków wyrażona wzorem:

.

Ostateczne rozwiązanie wygląda następująco:

,

.

Góra strony

2. Metody wykorzystujące szeregi potęgowe Legendre’a.

Polegają na rozwinięciu w szereg Maclaurina różnic względem parametru naturalnego, czyli długości linii geodezyjnej s.

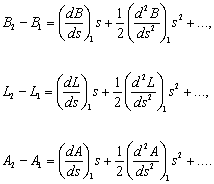[14]

Występujące w tych wzorach pochodne wyższych rzędów względem ds wyznacza się przez różniczkowanie równań pierwszego rzędu. Powolna zbieżność szeregów limituje ich wykorzystanie do odległości nie przekraczających 150 kilometrów.”

Szczególnie znaną i powszechnie stosowaną metodą przede wszystkim w przypadku dotyczącym zadania odwrotnego, jest metoda średniej szerokości Gaussa. Według niej wprowadza się do szeregów potęgowych Legendre’a punktu o szerokości B_m, odpowiadającej punktowi usytuowanemu w połowie długości linii geodezyjnej s pomiędzy punktami P₁ i P₂. Można tę metodę stosować dla odległości do 200 kilometrów.

Góra strony

2.1. Metoda średniej szerokości Gaussa - zadanie wprost

Początkowa forma metody została opracowana w 1846 roku przez F.C. Gaussa. Z biegiem czasu kilkakrotnie ją unowocześniano w celu rozszerzenia zakresu stosowalności dla większych odległości i szerokości geograficznych. Jej użycie to nic innego niż wykorzystaniu szeregów potęgowych Legendre’a ale nie w postaci [14], gdzie pochodne względem parametru naturalnego s odnosi się do punktu początkowego P₁ , lecz do pewnego pomocniczego punktu P_m usytuowanego w połowie długości linii geodezyjnej.

Spłaszczenie elipsoidy sprawia, że współrzędne punktu P_m i azymut linii w tym punkcie są na ogół różne od wartości średnich.

, , , , , ,

gdzie:

B – szerokość geodezyjna średnia,

L – długość geodezyjna średnia,

B_m, B₁, B₂ – szerokości geodezyjne odpowiednich punktów,

L_m, L₁, L₂ – długości geodezyjne odpowiednich punktów,

A₁, A₂ – azymuty.

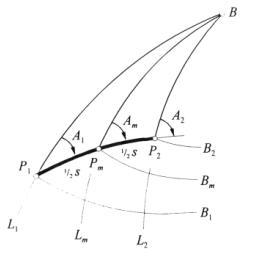
Rys. 6 Pomocniczy punkt Gaussa w połowie długości s.

Rozwinięcie różnic B₂ - B_m i B₁ – B_m w szereg potęgowy według propozycji Gaussa przyjmie postać:

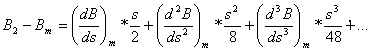, [15]

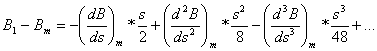. [16]

Wiedząc, że wzrost wartości parametru s ma miejsce w kierunku od P1 do P₂, przyrost s P_m P₁ należy uznać za ujemny. Znaki ‘-‘ przy wyrazach

zawierających nieparzyste potęgi s są tego wynikiem. Wyrażenia analogiczne do [15], [16] moglibyśmy napisać dla L₂-L_m i L₁-L_m oraz dla A₂-A_m i A₁-A_m.

Tworząc różnice równań [15] i [16] oraz analogicznych równań dla długości i azymutów otrzymamy:

,

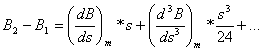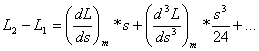, [17]

,

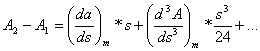gdzie:

s – długość linii geodezyjnej,

tworząc zaś sumy tych równań i dzieląc je przez 2 otrzymamy:

,

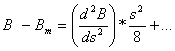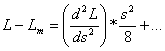, [18]

.”

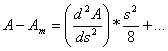Kiedy spojrzymy na wzory [17] i porównamy je z wzorami [14], zauważymy, że wzory Gaussa zawierają tylko pochodne nieparzystego rzędu. Wiemy zatem, że są prawie o połowę krótsze. Ponadto współczynniki przy odpowiednich pochodnych w tych wzorach są mniejsze.

Podstawowy problem to wyznaczenie wartości pochodnych w punkcie P_m, którego współrzędnych nie znamy. Z wzorów [18] otrzymamy, że różnice B-B_m, L-L_m i A-A_m to wielkości małe drugiego rzędu względem B₂-B₁, L₂-L₁ i A₂-A₁. Toteż Gauss proponuje zastąpienie pochodnych w punkcie P_m rozwinięciem w szereg Taylora w otoczeniu punktu p, zachowując tylko wyrazy pierwszego rzędu w tym rozwinięciu. Czyli, że:

,

, [19]

.

Jeśli zróżniczkujemy wzory

, , [20]

względem B i A, a wyniki różniczkowania podstawimy do [19], pozostaną nam jeszcze B_m, L_m i A_m w różnicach (B_m-B), (L_m-L), (A_m-A). Zanim zastąpimy je wyrażeniami [20], dla których drugie pochodne powinny być wyznaczone w punkcie P_m, zauważmy iż pomimo, że wyrażenia te są wielkościami małymi drugiego rzędu, to zaniedbaliśmy w nich wyrazy czwartego rzędu (wyrazy trzeciego rzędu wchodzą do wyrażeń [17]).

Wobec tego pochodne w [18] wyznaczymy w punkcie P, tzn.:

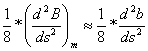
i analogicznie dla L i A. W ten sam sposób podejdziemy do pochodnych wyższych rzędów (trzeciego i piątego) w punkcie P_m w wyrażeniach [17]. Obliczymy wartości tych pochodnych dla szerokości, długości i azymutu. Będą one średnimi arytmetycznymi odpowiednich wartości w punktach P₁ i P₂.

Widzimy, że po wykonaniu opisanego różniczkowania, po podstawieniu wyników do wzorów [19], a następnie podstawieniu tych wzorów do [17], po zastąpieniu w [17] pochodnych wyższych rzędów w punkcie P_m pochodnymi w punkcie P, otrzymamy wzór Gaussa dla różnic (B₂-B₁), (L₂-L₁) i (A₂-A₁). W końcowych wzorach zachowano przede wszystkim wyrazy małe czwartego rzędu, a także wyrazy zawierające , a nawet . Pozbyto się natomiast wyrazów, w których pojawiły sięitd. Wzory takie stosuje się w przypadku s dochodzących do 200 km, otrzymując dokładność obliczeń 0,0001’’ dla szerokości i długości oraz 0,001’’ dla azymutu.

W otrzymanych w ten sposób (na podstawie ogólnego zapisu [17]) wzorach zastosowano następujące oznaczenia:

, ,

, ,

a także V przedstawione wzorem:

.

Ostatecznie wzory maja postać:

,

,

,

,

, [21]

.

W przypadku, kiedy do rozwiązania jest zadanie wprost należy zastosować postępowanie iteracyjne, gdyż po prawych stronach wzorów występują nieznane b i l. Wystarczy wyjściową wartość tych wielkości pomierzyć na mapie topograficznej (), aby po dwóch krokach iteracyjnych uzyskać wyniki z zadowalającą dokładnością.

Góra strony

2.2. Metoda średniej szerokości Gaussa zadanie odwrotne.

Zadanie odwrotne rozwiązujemy metodą Gaussa po ‘odwróceniu’ wzorów. Dokonujemy tego następująco:

,

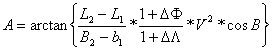. [22]

Ze wzoru [22] obliczymy wartość , zaś korzystając z [21] obliczymy wartość różnicy azymutów . Interesujące nas azymuty ‘wprost’ i ‘odwrotny’ będą się wyrażały następująco:

.,

Metoda ta była najczęściej stosowana właśnie do rozwiązania odwrotnego zadania geodezji wyższej.

Ostateczne rozwiązanie:

,

, .

Góra strony

3. Metody bezpośrednie.

Polegają one na rozwiązaniu trójkąta elipsoidalnego a jego dwa punkty są punktami początkowym i końcowym linii geodezyjnej P₁ i P₂, natomiast punkt trzeci jest biegunem elipsoidy.

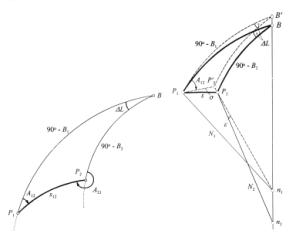
Rys. 7 Duży trójkąt geodezyjny i jego rzut na sferę pomocniczą.

W metodach bezpośrednich stosowano pomocniczą kulę o promieniu N₁ lub a i środku w n₁. Punkty P₁ i B rzutowano na tę kulę tak, aby niektóre elementy trójkąta pozostały niezmienione. Aby uzyskać końcowe rozwiązanie zajmowano się trójkątem sferycznym, a wyznaczone elementy przenoszono na elipsoidę. Jako przykład służą metody Bessela z roku 1826 i Helmerta z roku 1880, w których trójkąt P₁P₂B został odwzorowany na kulę o promieniu a w taki sposób, aby szerokości zredukowane były równe szerokościom na kuli. W odwzorowaniu azymutów zachowano wierność przez wykorzystanie równania Clairauta dla linii geodezyjnej. Zniekształceniu ulegają długość linii geodezyjnej s i różnica długości geodezyjnych . Różniczki pierwszego rzędu na kuli (względem długości odpowiadającej s) odpowiednie do

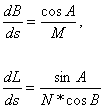
na elipsoidzie przedstawiamy następująco

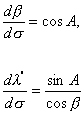
można je przekształcić do postaci:

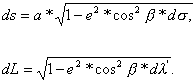
Całkowanie powyższych równań prowadziłoby do całek eliptycznych. Po rozwinięciu w szeregi, wykonaniu całkowania wyraz po wyrazie, a następnie odwróceniu szeregów wyprowadzono wzory dla metody Bessela.

Góra strony

3.1. Metoda Bessela zadanie wprost

Metoda Bessela przenoszenia współrzędnych może być stosowana w stosunku do bardzo dużych odległości dochodzących nawet do 20 tysięcy kilometrów. Wykonanie zadania przeniesienia współrzędnych na podstawie tej metody polega na przeniesieniu rozwiązania z elipsoidy o znanych parametrach na kulę o promieniu R = a, wykorzystaniu szerokości zredukowanej u, rozwiązania zadania na kuli i przeniesieniu wyników z powrotem na elipsoidę.

Pomiędzy wielkościami na kuli i odpowiednimi do nich wielkościami na elipsoidzie mamy następujące zależności:

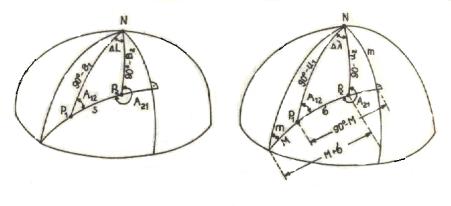
Rys. 8 Oznaczenia wielkości na elipsoidzie i na odpowiadającej jej kuli.

Na rysunku przedstawiono zasadę przenoszenia współrzędnych na elipsoidzie i na odpowiadającej jej kuli oraz oznaczenia występujących wielkości.

W celu rozwiązania zadania przenoszenia współrzędnych na kuli, należy uprzednio obliczyć nieznane wartości i .

Na elipsoidzie obrotowej o parametrach a, e² dane są: współrzędne geodezyjne punktu P₁(B₁,L₁), azymut linii geodezyjnej A₁₂ z punktu P₁ na P₂ oraz odległość s między nimi.

Obliczane wielkości to współrzędne geodezyjne punktu P₂(B₂,L₂) oraz azymut A₂₁ z punktu P₂ na P₁.

Kolejność rozwiązywania takiego zadania przedstawia się następująco:

a) Przelicza się szerokość geodezyjną na szerokość zredukowaną (B₁ na u₁)

,

b) oblicza się też odległość na kuli między pozycją P₁ i P₂

gdzie:

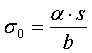
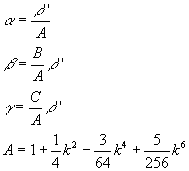
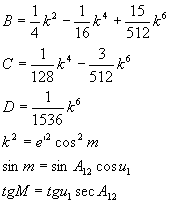
c) oblicza się azymut odwrotny A₂₁

,

d) oblicza się szerokość zredukowaną u₂

,

e) zamienia się szerokość zredukowaną na szerokość geodezyjną B₂

,

f) oblicz się wartość

,

g) oblicza się wartość

,

gdzie:

.

h) oblicza się wartość L₂

W wyniku takiego postępowania otrzymamy:

B₂, L₂, A₂₁

Góra strony

3.2. Metoda Bessela zadanie odwrotne

Na elipsoidzie obrotowej o parametrach a, e² mamy dane współrzędne geodezyjne punktu P₁(B₁,L₁) oraz punktu P₂(B₂,L₂). Obliczyć musimy długość linii geodezyjnej s oraz jej azymuty w punkcie P₁ i P₂, czyli azymuty wprost A₁₂ oraz odwrotny A_21.

Kolejność wykonywania zadania wygląda następująco:

a) Przeliczamy szerokość geodezyjną B₁ i B₂ na szerokość zredukowaną u₁ i u₂

,

,

gdzie:

e – pierwszy mimośród elipsoidy,

b) obliczamy różnicę długości, szerokości oraz szerokość średnią,

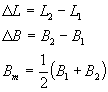
c) obliczamy różnicę długości na kuli (pierwsze przybliżenie)

gdzie:

Dokładne wartości dla dużych odległości (powyżej 1000 km) liczymy wykorzystując uprzednie przybliżenie oraz

- współczynniki, które zostały już przedstawione w schemacie rozwiązania zadania wprost

Ostateczną wartość wyliczymy

gdzie:

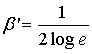
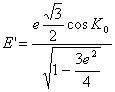
Następnie wyliczamy

lub z uprzedniego wzoru

d) obliczamy azymut wprost A₁₂ i azymut odwrotny A₂₁ linii geodezyjnej

e) obliczamy też długość linii geodezyjnej s

gdzie:

A, B, C, - przedstawiono w schemacie rozwiązania zadania wprost.

W wyniku takiego postępowania otrzymamy:

.

Góra strony

4. Metody wykorzystujące cięciwy elipsoidy.

4.1. Metoda Mołodeńskiego

M. S. Mołodeński zaproponował obliczanie współrzędnych za pomocą cięciw elipsoidy. Niekonwencjonalne, trójwymiarowe podejście Mołodeńskiego wymagało nowych definicji podstawowych wielkości geodezyjnych. Odległością s₁₂ dwóch punktów na elipsoidzie nazywa Mołodeński długość odcinka prostej-cięciwy elipsoidy przechodzącej przez te punkty. Azymutem geodezyjnym cięciwy (A₁₂) autor metody nazywa kąt dwuścienny, jaki tworzy płaszczyzna południka geodezyjnego punktu P₁ z płaszczyzną wertykalną tego punktu zawierającą cięciwę P₁P₂. Mołodeński posługuje się także odległością zenitalną cięciwy. W konsekwencji tych definicji autor traktuje trójkąty płaskie utworzone z cięciw elipsoidalnych jako trójkąty geodezyjne nowego typu.

Rozwiązanie zadań wprost i odwrotnego według Mołodeńskiego polega na rozwiązaniu trójkątów sferycznych Z₁Z₂B i Z₁BK, przy czym K jest śladem cięciwy P₁P₂ na sferze o promieniu jednostkowym zatoczonej w punkcie P₁.

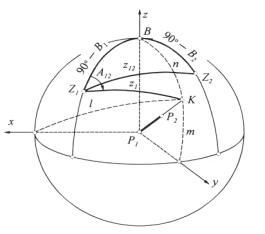
Rys. 9. Kula jednostkowa w punkcie P₁ objaśniająca metodę Mołodeńskiego.

Współrzędne, które przelicza się do innego układu odniesienia należy uzupełnić o poprawki dφ, dλ, dH, które uwzględnia Mołodeński w swojej metodzie. Dzięki znajomości przesunięć środków elipsoid możliwe jest przeliczanie współrzędnych z jednego układu odniesienia do drugiego. Przeliczanie to rozbija się na dwa warianty:

- przeliczanie współrzędnych określanych w oparciu o różne lokalne układy odniesienia,

- przeliczanie współrzędnych określanych w układzie lokalnym do układu geocentrycznego lub na odwrót.

Dzięki metodzie opartej na wzorach Mołodeńskiego otrzymujemy wartości przyrostów dj, dl, dh przy przejściu od układu lokalnego do układu geocentrycznego (globalnego) lub odwrotnie. Wzory pochodzą z: Thomas A. Stansell: Navigation Satellite System – Magnavox 1978 i Instrukcja odbiornika GG 24 firmy Astech.

j_k = j + Dj

l_k = l + Dl

H_k = H + DH

gdzie:

j, l, H - współrzędne geograficzne punktu w starym układzie,

j_k, l_k, H_k – współrzędne geograficzne punktu w nowym układzie po przeniesieniu współrzędnych.

Wzory Mołodeńskiego podają poprawki na różnicę współrzędnych ∆φ, ∆λ, ∆H celem przejścia z układu współrzędnych geocentrycznych do innego układu odniesienia lub odwrotnie.

Dj” = [-DX sinj cosl - DY sinj sinl + DZ cosj + aDf + fsin2jDa]

Dl” = - (DX sinl + DY cosl)

DH = DX cosj cosl + DY cosj sinl + DZ sinj + (a Df + f Da) sin²j - Da

gdzie:

ρ’’- 206264,806246- wartość radiana wyrażona w sekundach,

j, l, H - współrzędne geograficzne punktu,

Dj, Dl, DH

- poprawki dla dokonania transformacji ze starego układu odniesienia do nowego układu odniesienia,

DX, DY, DZ - poprawki współrzędnych prostokątnych przestrzennych,

a - duża półoś elipsoidy lokalnej,

b - mała półoś elipsoidy lokalnej,

f= - spłaszczenie elipsoidy lokalnej,

Da, - różnica wartości dużych osi elipsoidy,

Df - różnice spłaszczeń elipsoid,

e - pierwszy mimośród elipsy południkowej:

e² = ,

N - promień krzywizny pierwszego wertykału:

,

M - promień krzywizny południka:

.

Wszystkie wartości D powstają poprzez odjęcie wartości parametrów starej elipsoidy od wartości parametrów elipsoidy nowej.

Góra strony

Bibliografia:

1. Banachowicz A. Urbański J., „Obliczenia nawigacyjne”, Akademia Marynarki Wojennej, Gdynia, 1987.

2. Baran W., „Teoretyczne podstawy opracowania wyników pomiarów geodezyjnych”, Warszawa, 1990.

3. Czarnecki K. „Geodezja współczesna w zarysie”, Gdynia, 1999.
4. Felski A., Urbański J., „Uwzględnianie wpływu układu odniesienia na współrzędne pozycji”, Gdynia 1984.

5. Górski S., „Ocena dokładności w nawigacji morskiej”, Gdańsk, 1977.

6. Gucma S., „Podstawy teorii linii pozycyjnych i dokładności w nawigacji morskiej”, Wyższa Szkoła Morska, Szczecin, 1995.

7. Stateczny A, Urbański J., Kantak, „Podstawy automatyzacji nawigacji. Część A”, Wyższa Szkoła Morska, Gdynia, 1988.

8. Urbański J., Czapczyk M., „Podstawy kartografii i geodezji nawigacyjnej”, Wyższa Szkoła Morska, Gdynia, 1988.

9. Urbański J., Januszewski J., „Podstawy nawigacji satelitarnej”, Wyższa Szkoła Morska, Gdynia, 1992.

Góra strony