Wybrane odwzorowania kartograficzne

Na początek kilka słów wstępu......

Mapy (w tym morskie) umożliwiają nam spojrzeć na całą ziemię, jednocześnie pozwalają stworzyć szczegółowy obraz jej części (basen portowy). Termin mapa pochodzi od łacińskiego słowa mappa, które oznaczało zmniejszone, uogólnione przedstawianie na powierzchni płaszczyzny całości lub fragmentu powierzchni ziemi.

Kartografia jest to nauka dotycząca sporządzania, powielania i o wykorzystaniu map. Definicja Brytyjskiego Towarzystwa Kartograficznego z 1964 podaje, że jest to nie tylko nauka i technologia, ale też sztuka sporządzania map oraz ich badanie jako dokumentów naukowych, a także dzieł sztuki.

Klaudiusz Ptolemeusz, w II w.p.n.e., jako pierwszy podjął się kartograficznemu przedstawieniu Ziemi. Jednakże dopiero na początku XX w., kartografię zaczęto traktować jako samodzielną naukę, a nie jak wcześniej dział geodezji.

Poważnym krokiem naprzód w rozwoju kartografii wywarła fotogrametria lotnicza.

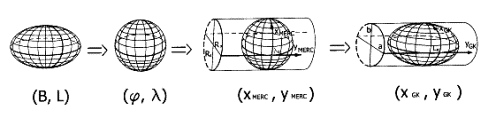
Zarówno rzuty jak i odwzorowania kartograficzne, są sposobami przedstawienia Ziemi w taki sposób, aby każdemu punktowi na naszym globie odpowiadał punkt na mapie.

Konstrukcja rzutów oparta jest na działaniach matematycznych, które określają zależności pomiędzy współrzędnymi geograficznymi punktów na powierzchni Ziem (traktowanej jako obrotowa elipsoida), a współrzędnymi płaskimi x i y obrazu tego punktu w przyjętym odwzorowaniu.

Mimo rozwoju techniki nie ma odwzorowania, w którym byłyby wyeliminowane wszystkie zniekształcenia. Każde z nich zawiera zniekształcenia długości, kątów bądź powierzchni.

Odwzorowanie kartograficzne polega na przeniesieniu położenia punktów z powierzchni odniesienia (powierzchni kuli lub elipsoidy ziemskiej) na płaszczyznę mapy z zastosowaniem określonych reguł matematycznych. Praktycznie jest to przeniesienie siatki geograficznej, która jest podstawą określania położenia punktów na Ziemi.

Siatkę kartograficzną tworzy się z obrazu siatki geograficznej przedstawionej na mapie z zachowaniem reguł odwzorowania. Podstawą do otrzymania siatki kartograficznej są przeliczenia matematyczne określające miejsca przecięcia się odpowiednich południków i równoleżników, bądź rzutowanie geometryczne siatki geograficznej na płaszczyznę, ewentualnie walec lub stożek. Jeżeli dany punkt zrzucimy na płaszczyznę uzyskamy jeden punkt, jeżeli na walec lub stożek jedną linię, które odwzorowują się wiernie bez zniekształceń kartograficznych. Wynika to z tego, iż kulistej powierzchni nie można rozwinąć na płaszczyznę bez rozerwania jej ciągłości i bez zniekształceń.

Skala mapy i rodzaj odwzorowania, położenia obszaru w stosunku do punktu lub linii stycznej są bezpośrednimi czynnikami wpływającymi na wielkość i charakter zniekształceń. Widzimy to wyraźnie porównując siatkę kartograficzną i geograficzną. Poprzez wykorzystanie działań matematycznych obrazy siatki geograficznej i kartograficznej są zbieżne. Pomimo różnic wizualnych, na mapie możemy dokonywać pomiarów i określać położenie geograficzne punktów, a przebieg równoleżników i południków na mapie wiernie odwzorowują główne kierunki.

Istnieje wielka różnorodność odwzorowań kartograficznych, które posiadają zarówno swoje pozytywne jak i negatywne cechy, które wynikają głównie z występowania zniekształceń kartograficznych.

W żadnym z odwzorowań nie można uzyskać wiernego przedstawienia odległości na całej mapie. Możliwe jest to tylko wzdłuż pewnych kierunków i takie odwzorowanie nazywa się wiernoodległościowym. Natomiast niektóre z odwzorowań mają taki rozkład zniekształceń odległości, że przedstawione są w nich wiernie kąty (kierunki) – są to odwzorowania wiernokątne – lub pola powierzchni figur – odwzorowania wiernopowierzchniowe.

Istnieją jeszcze odwzorowania dowolne – są to takie, które nie zachowują ani wierności kątów, ani powierzchni, ani też odległości. Siatki klasyczne, są to takie, które można skonstruować przez rzutowania geometryczne. Ze względu na to, na jaką powierzchnię rzutuje się siatkę kartograficzną, wyróżnia się odwzorowania i siatki kartograficzne: azymutalne, walcowe i stożkowe, które przedstawione są poniżej.

Źródło promieni rzutujących może znajdować się w różnej pozycji w stosunku do punktu styczności płaszczyzny – w środku kuli (rzut gnomoniczny), na antypodach punktu styczności (rzut stereograficzny) lub w nieskończoności (rzut ortograficzny).Wyróżniamy trzy położenia siatki kartograficznej: położenie normalne, poprzeczne i ukośne. Zależy to od położenia punktu lub linii styczności płaszczyzny lub figury na kuli ziemskiej. W położeniu normalnym osie stożka i walca są zgodne z osią biegunową Ziemi, a płaszczyzna jest prostopadła do osi obrotu Ziemi. Gdy osie stożka lub walca są zgodne z jedną z osi równika, a punkt styczności płaszczyzny jest położony na równiku, mamy wtedy do czynienia z odwzorowaniem poprzecznym. Inaczej jest w odwzorowaniu ukośnym, położenie osi walca oraz punktu styczności jest pośrednie - pomiędzy biegunami a równikiem.

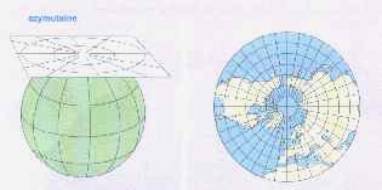
. Rys. 1. Odwzorowanie azymutalne

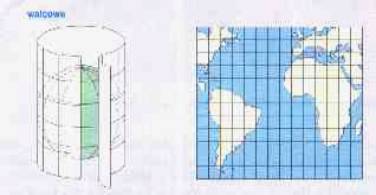
Rys. 2. Odwzorowanie walcowe

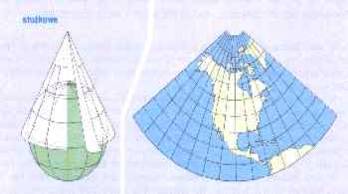
Rys. 3. Odwzorowanie stożkowe

Poniżej przedstawiono wszystkie trzy powyższe odwzorowania czyli, azymutalne , walcowe i stożkowe w odwzorowaniu ukośnym i poprzecznym.

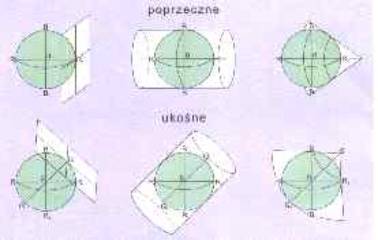
Rys. 4. Odwzorowanie poprzeczne i ukośne

W celu zmniejszenia zniekształceń stosuje się również rzutowanie na powierzchnie sieczne..w..stosunku..do..kuli.
Zastosowana kombinacja rodzaju powierzchni rzutowania, położenia źródła promieni rzutujących i punktu (linii) styczności staje się odrębnym odwzorowaniem. Decyduje o kształcie południków i równoleżników, odległościach i kątach pomiędzy nimi, a więc o charakterze i rozkładzie zniekształceń na mapie.

W siatce płaszczyznowej, w normalnym położeniu, południki odwzorowane są jako proste, które rozchodzą się od bieguna w sposób promienisty natomiast równoleżniki w postaci współśrodkowych okręgów. Odległości między równoleżnikami zależą od położenia źródła promieni rzutujących.

W siatkach walcowych, w położeniu normalnym, południki i równoleżniki są liniami prostymi i tworzą sieć prostokątów. Istotne tutaj jest, że odległości pomiędzy południkami są rzeczywiste tylko na równiku (zgodnie ze skalą mapy) W odróżnieniu od siatki geograficznej, odległości między południkami pozostają takie same na całym arkuszu mapy.

W siatce stożkowej, w położeniu normalnym, rozwinięty stożek ma kształt wycinka koła. Południki zbiegają się we wspólnym punkcie, który zazwyczaj nie jest przedstawiony na mapie (najczęściej bieguny). Południki ukazane są jako linie proste, równoleżniki z kolei jako współśrodkowe łuki.

Odwzorowanie wybieramy w zależności od obszaru i zakresu wykorzystania danej mapy. Jeżeli planujemy podróż oceaniczną, wybieramy mapę o małej skali z odwzorowaniem o bardzo małych zniekształceniach odległości. Jeżeli uprawiamy żeglugę przybrzeżną lub na małych odległościach, wybieramy mapy wiernokątne i wiernopowierzchniowe, pamiętając o zniekształceniach odległości..

1.Odwzorowanie Merkatora

Podstawowym odwzorowaniem kartograficznym stosowanym do opracowania map nawigacyjnych jest normalne wiernokątne odwzorowanie walcowe, zwane powszechnie odwzorowania Merkatora. Zostało ono wstępnie opracowane w 1569 roku przez flamendzkiego kartografa Gerharda Kremera (1512—1594) zwanego po łacinie Merkatorem, twórcy nowoczesnej kartografii. W 1569 wydał mapę świata w opracowanym przez siebie rzucie, zwanym rzutem Merkatora. Wprowadził pojęcie atlasu - nazwał tak zbiór map, który wydał w latach 1585-1595.

Odwzorowanie to, w późniejszych latach było modyfikowane przez E.Wrighte’a i J.Gregory’ego.

W odwzorowaniu Merkatora teoretyczny walec styka się z powierzchnią kuli wzdłuż równika. Charakterystyczne w tym odwzorowaniu jest to że, południki przecinają się z równoleżnikami pod stałym kątem, przy czym odległości między południkami są stałe i proporcjonalne do odpowiednich im różnic długości geograficznych na powierzchni elipsoidy (kuli). Występuje tu podstawowe założenie wiernokątności, czyli siatka kartograficzna normalnego odwzorowania walcowego jest siatką prostokątną, a pola powierzchni zwiększane są coraz to bardziej w miarę wzrostu szerokości geograficznej, przez co ma ono niewielkie zastosowanie poza nawigacją.

Rys. 5. Siatka kartograficzna w normalnym odwzorowaniu walcowym

Przy takim odwzorowaniu, loksodroma (linia łącząca dwa dowolne punkty znajdujące się na płaszczyźnie tego odwzorowania) jest linią prostą, która przecina południki pod jednakowym kątem. Natomiast ortodroma jest tu krzywą wygiętą w kierunku bieguna (krótszy łuk koła wielkiego). Koło wielkie na mapie Merkatora jest krzywą sinusoidalną, którą w połowie jest na N, a w połowie na S – wygięta jest po prostu w kierunku bliższego bieguna.

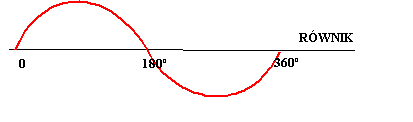
Rys. 6 Koło wielkie na mapie Merkatora

Funkcje normalnego odwzorowania walcowego dla walca stycznego mają postać;

gdzie:

a- stały współczynnik równy dłuższej półosi elipsoidy ziemskiej

Pierwsze z wyrażeń, czyli X=f(φ) jest równaniem równoleżników, natomiast wyrażenie Y=aλ to równanie południków. Skale wzdłuż południków (m) oraz wzdłuż równoleżników (n) ustala się z zależności takich jak:

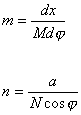
gdzie:

dx – różniczka współrzędnych prostokątnych

dφ – przyrost szerokości geograficznej

a – duża półoś elipsoidy

N – promień przekroju pierwszego wertykału

M – promień krzywizny przekroju południowego

Aby odwzorowanie spełniało warunek wiernokątności musi występować zależność:

m=n , czyli

Na podstawie równań południkowych i równoleżnikowych oraz przy uwzględnieniu powyższej zależności otrzymuje się:

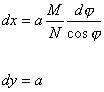
z tego wynika, że funkcje odwzorowawcze przyjmują postać:

Przy odwzorowaniu Merkatora należałoby wspomnieć o powiększonej szerokości. Definicja powiększonej szerokości mówi, że jest to odległość na mapie w odwzorowaniu Merkatora od równika do równoleżnika żądanej szerokości geograficznej φ, wyrażana w minutach długości geograficznej.

W kartografii nawigacyjnej wartość funkcji X oznacza się poprzez V i nazywa się ją powiększoną szerokością oraz przedstawia się następującym wzorem:

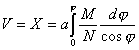
Podstawiając wzory na M i N otrzymujemy:

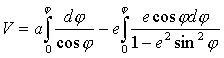
Przy obliczaniu siatki kartograficznej tegoż odwzorowania należy rozwiązać jedno z dwóch zadań. Pierwsze zadanie polega na obliczeniu siatki kartograficznej rejonu, którego granice są dokładnie określone równoleżnikami i oraz południkami i Drugie zadanie polega na obliczeniu siatki kartograficznej, którego granice są określane w przybliżeniu, ale ściśle oznaczona jest skala mapy.

Przy rozwiązywaniu każdego z powyższych zadań należy uwzględnić, wartości: szerokość i długość mapy. Jeżeli znany jest wewnętrzny wymiar arkusza mapy, to, aby rozwiązując pierwsze zadanie należy określić skalę mapy, która umożliwi przedstawienie wybranego obszaru powierzchni Ziemi na arkuszu o ustalonych wymiarach. Przy rozwiązywaniu drugiego zadania określa się równoleżniki i południki ograniczające rejon, który ma być przedstawiony na mapie w żądanej skali. Obliczając powiększoną szerokość w minutach długości geograficznej otrzymuje się jednakowe jednostki miary dla równoleżnikowej i południkowej ramki mapy.

Jednostką mapy nazywa się długość liniowa jednej minuty długości geograficznej na mapie w odwzorowaniu Merkatora, wyrażona w milimetrach. Jest ona uzależniona od skali mapy oraz od szerokości geograficznej równoleżnika podstawowego. Jednostką mapy rozpoczyna się obliczenie siatki kartograficznej. Jeżeli równoleżnikiem podstawowym jest równik i skalę główną mapy na nim oznaczy się jako 1:, wówczas jednostkę mapy oblicza się ze wzoru:

gdzie:

a – długość półosi rówikowej elipsoidy ziemskiej;

- mianownik skali mapy;

- wartość jednego radiana wyrażona w minutach

Jeżeli 1: jest skalą główną na równoleżniku podstawowym , to jednostkę mapy oblicza się ze wzoru:

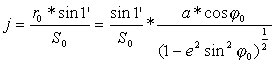
lub

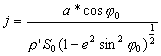(2.10)

gdzie:

ρ’ – wartośc jednego radiana wyrażona w minutach

Ze względu na zachowanie wiernokątności w tym odwzorowaniu nie może być ono używane na obszarach podbiegunowych. Spowodowane jest to tym, że w tych rejonach dochodzi do bardzo dużego powiększenia powierzchnii (bieguny odwzorowują się w nieskończoności).

Odwzorowanie Merkatora spowodowało przełom w nawigacji. Dzięki wiernokątności prowadzenie żeglugi według wskazań kompasu magnetycznego i żyrokompasu jest dużo łatwiejsze. Dodatkowym walorem jest zmienna skala odległości, która jest równoznaczna z kątową skalą szerokości geograficznej zamieszczoną na lewej i prawej ramce mapy.

2.Odwzorowanie Gaussa-Krűgera.

Odwzorowanie Gaussa-Krügera (jego angielski odpowiednik to Transverse Mercator Projection) jest to wiernokątne walcowe poprzeczne odwzorowanie elipsoidy. W tym odwzorowaniu, w celu jego zinterpretowania należy wyobrazić sobie walec styczny do elipsoidy na całej długości południka środkowego lub osiowego odwzorowania. Aby odwzorowanie było prawidłowe musi spełnić warunki takie jak:

wiernokątności,

prostoliniowości

izometryczności odwzorowania południka środkowego przy założeniu początku układu kartograficznego w punkcie przecięcia obrazu południka osiowego z obrazem równika.

Obraz południka jest osią odciętych zaś obraz równika jest osią rzędnych układu kartograficznego. Najbardziej efektywna metoda w/w warunków sprowadza się do trzech podstawowych etapów:

I. wiernokątne odwzorowanie całej powierzchni elipsoidy na całą sferę

II wiernokątne – walcowe – poprzeczne odwzorowanie sfery na płaszczyznę-odwzorowanie poprzeczne Merkatora

III wiernokątne przekształcenie płaszczyzny Merkatora na płaszczyznę Gaussa-Krügera, tak, aby był spełniony warunek odwzorowania dotyczący izometryczności południka środkowego.

Powyższe etapy przedstawia również poniższy rysunek.

Rys. 7 Schemat geometryczny realizacji odwzorowania Gaussa-Krügera

Gdybyśmy przyjęli, że Ziemia jest kulą a nie elipsoidą, cały problem sprowadzałby się do etapu drugiego a odwzorowanie Gaussa-Krügera i odwzorowanie poprzeczne Mercatora byłyby identyczne. Ogólny algorytm odwzorowania Gaussa-Krügera można zapisać następująco:

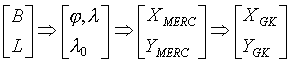
Wzory te również obejmują przekształcenia odwrotne:

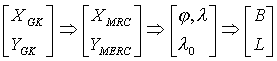
gdzie:

B , L – współrzędne geodezyjne punktu

φ i λ – odpowiadające współrzędne na sferze, przy czym λ = L

λo = Lo – długość geodezyjna południka środkowego w odwzorowaniu UTM, pokrywająca się z długością południka środkowego odwzorowania Gaussa-Krügera

XMERC, YMERC – współrzędne odwzorowania UTM

XGK, YGK – współrzędne odwzorowania Gaussa-Krügera

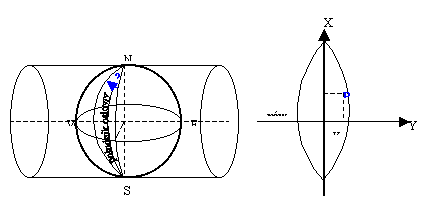
Rys. 8. Pas południkowy na powierzchni elipsoidy ziemskiej i na płaszczyźnie w odwzorowaniu Gaussa-Krügera

W odwzorowaniu Gaussa-Krügera obszar Ziemi należy podzielić na odpowiednie pasy południkowe, ponieważ obszaru całej powierzchni lub znacznej części elipsoidy nie można odwzorować bez dużych zniekształceń. Każdy z tych podziałów stanowi oddzielny układ współrzędnych prostokątnych płaskich. Szerokości pasów ustalone są tak, ażeby każdy z nich można było odwzorować na płaszczyznę (tj. przedstawić na mapie) bez praktycznie odczuwalnych zniekształceń, które nie przekraczałyby stopnia dokładności map. W tym celu powierzchnie elipsoidy obrotowej dzieli się, począwszy od zerowego południka Greenwich, na 60 pasów południkowych po 6º każdy lub 120 pasów po 3º każdy. Południk środkowy w każdym pasie nazywamy południkiem osiowym; dzieli on pas na dwie równe części: zachodnią i wschodnią.

Teoretycznie biorąc, mapy w odwzorowaniu Gaussa-Krügera są obarczone zniekształceniami długości i mają w różnych punktach mapy niejednakową skalę. Mimo to zniekształcenia te są tak małe, że skalę mapy w obrębie jednego arkusza można uważać za stałą. Najczęściej stosowane są pasy południkowe 3º i 6º długości geograficznej. Pasy 3-stopniowe obejmują mniejsze obszary, zapewniają uzyskanie mniejszych zniekształceń, co jest szczególnie ważne dla triangulacji, gdyż zniekształcenia na styku dwóch układów wynoszą zaledwie 17 cm na 1000 m. Pasy 6-stopniowe długości geograficznej mają tę zaletę, że pozwalają odwzorować obszar dwa razy większy niż pasy 3-stopniowe, zmniejszając do połowy liczbę styków siatek kilometrowych, jak również zmniejszają liczbę ewentualnych źródeł błędów przy najzupełniej wystarczającej dokładności liniowej. W Polsce osnowa geodezyjna ze względu na potrzebę dokładności jest wykonywana w pasach 3-stopniowych, a mapy - w pasach 6-stopniowych. Odwzorowanie to można traktować jako rozwinięcie poprzecznego odwzorowania Merkatora przez zastąpienie powierzchni kuli powierzchnią elipsoidy obrotowej.

Z tego względu odwzorowanie Gaussa-Krűgera jest nazywane odwzorowaniem walcowym poprzecznym równokątnym powierzchni elipsoidy obrotowej.

W tabeli nr 2.1. przedstawione są wzory dla elipsoidy GRS-80 oraz dla elipsoidy Krassowskiego. Tabela nr 2.2. przedstawia niezbędne parametry obu tych elipsoid. Wynika z niej, że w ostatnim etapie przekształcenia „wprost” oraz w pierwszym etapie przekształcenia odwrotnego stosowany jest wielomian zmiennej zespolonej. Aby wykonać procedurę odwzorowawczą należy zadać długość geodezyjną Lo południka środkowego. Pozostałe procedury odwzorowawcze określa geometria danej elipsoidy.

Wzory w odwzorowaniu „wprost” wyrażają się bezpośrednio za pomocą znanych funkcji elementarnych i przestępnych. W odwzorowaniu odwrotnym należy zastosować szereg trygonometryczny, wielkość Lo oznacza taki promień, której długość południka idealnie odpowiada długości elipsy.

ODWZOROWANIE GAUSSA-KRŰGERA (B,ΔL)↔(XGK,YGK),

ΔL=L-L0

Tabela 1. Wzory dla elipsoidy GRS-80 i elipsoidy Krassowskiego

ALGORYTM..PRZEKSZTALCENIA „WPROST”

(B,ΔL)→(XGK,YGK)

ALGORYTM..PRZEKSZTAŁCENIA ”ODWROTNEGO”

(XGK,YGK)→(B,ΔL)

I Lagrange’a (B,ΔL)→(φ,Δλ)

III’ (φ,Δλ)→(B,ΔL)

U=1-e*sin(B), V=1+e*sin(B)

K=(U/V), C=K*tg(B/2+л/4)

(л=3,141592653589793)

φ=2*arctg(C)-л/2

Δλ=ΔL (przyrost względem L0)

m1=R0*cos(φ)/[Rn*cos(B)], γ1=0

B=φ+c2*sin(2*φ)+c4*sin(4*φ)+c6*sin(6*φ)

ΔL=Δλ

II Merkatora (φΔλ)→(XMERC,YMERC)

II’ (XMERC,YMERC)→(φ,Δλ)

p=sin(φ), q=cos(φ)*cos(Δλ)

r=1+cos(φ)*sin(Δλ)

s=1-cos(φ)*sin(Δλ)

XMERC=R0*arctg(p/q)

YMERC=0,5*R0*In(r/s)

m2=1/[r*s], γ2=arctg[p*tg(Δλ)]

α=XMERC/R0,

β=YMERC/R0

w=2*arctg[exp(β)]-π/2

φ=arcsin[cos(w)*sin(α)]

Δλ=arctg[tg(w)/cos(α)]

III (XMERC,YMERC)→(XGK,YGK)

I’ (XGK,YGK)→(XMERC,YMERC)

Z=[(XMERC-xo)*s, YMERC*s]

ZGK=a0+Z(a1+Z(a2+Z(a3+Z(a4+

+Z(a5+Za6)))))

ZGK=(XGK,YGK)

m3=;

γ3=-arctg(f/f)=-arcsin(f/m)

Z=[(XGK-a0)*s, YGK*s]

ZMERC=b0+Z(b1+Z(b2+Z(b3+Z(b4+

+Z(b5+Zb6)))))

ZMERC=(XMERC,YMERC)

ODWZOROWANIE..GAUSSA-KRŰGERA.– PARAMETRY..PROCEDUR

[Zastosowanie wielomianów dopuszczalne dla:B od 48º do 56º i L od-6º do+6º]

Tabela 2. Parametry elipsoidy GRS-80 i elipsoidy Krassowskiego

PROCEDURA OBJAŚNIENIE	PARAMETR NAZWA	ELIPSOIDA GRS-80	KRASOWSKIEGO
(B,Δλ)→(φ,Δλ)→(XMERC,YMERC)
- pierwszymimośród elipsoidy	e	0,0818191910428	0,0818133340169
- półosie elipsoidy	a	6378137	6378245
	b	6356752,31414	6356863,01877
- spłaszczenie	f	1:298,257222101	1:298,3
- promień sfery Lagrange’a	R0	6367449,14577	6367558,496875
(XMERC,YMERC)→(XGK,YGK)
- parametr normujący	s	2,0E-6	2,0E-6
- parametr centrujący	x0	5760000	5760000
- współczynniki wielomianu	ao	5765181,11148097	5765180,4975833
	a1	499800,81713800	499800,87112376
	a2	-63,81145283	-63,80172299
	a3	0,83537915	0,835512434
	a4	0,13046891	0,13044472
	a5	-0,00111138	-0,00111100
	a6	-0,00010504	-0,00010501
(XGK,YGK)→(XMERC.YMERC)
- parametr normujący	s	2,0E-6	2,0E-6
- parametr centrujący	x0’=a0	5765181,11148097	5765180,4975833
- współczynniki wielomianu	b0	5760000	5760000
	b1	500199,26224125	500199,20821246
	b2	63,88777449	63,87801231
	b3	-0,82039170	-0,82014111
	b4	-0,13125817	-0,13123362
	b5	0,00101782	-0,00101747
	b6	0,00010778	0,00010775
(φ,Δλ)→(B,Δλ)
-współczynniki szeregu trygonometrycznego	c2	0,0033565514856	0,0033560696018
	c4	0,0000065718731	0,0000065699863
	c6	0,0000000176466	0,0000000176390
	c8	0,0000000000540	0,0000000000540

Odwzorowanie Gaussa-Krügera sprowadzono ostatecznie do dwukierunkowo działającej formuły:

(B , ∆L) ó (XGK, YGK), przy czym ∆L = L – Lo

Parametrem lokalizującym odwzorowania Gaussa-Krügera jest długość geodezyjna południka środkowego oznaczona jako Lo.

Na przykładzie rysunku 9. wynika, że:

odcięta XGK jest mierzona względem obrazu równika jako osi Oy płaskiego układu,

rzędna YGK względem obrazu południka środkowego jako osi Ox tegoż układu.

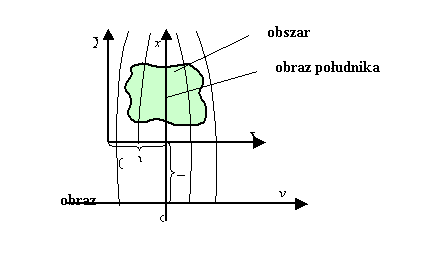
Rys. 9 Ogólna zasada aplikacji odwzorowania Gaussa-Krügera

Objaśnienia do powyższego rysunku

- układ współrzędnych Gaussa-Krügera

OXY- układ aplikacyjny

mo – skala podobieństwa

- składowe przesunięcia

Wielkość mo zwana skalą na południku środkowym, pełni równocześnie funkcję skali prawdopodobieństwa konkretnej aplikacji względem oryginalnego odwzorowania Gaussa-Krügera.

Jeśli mo <1 to parametr ten ma na celu równomierne rozłożenie bezwzględnych wartości zniekształceń liniowych odwzorowania. Parametr przesunięcia układu współrzędnych oznaczone xo i yo mają zasadniczo dwa cele:

- w przypadku yo chodzi o to, aby zapobiec występowaniu ujemnych wartości rzędnych lub szczególne wyróżnienie danej strefy układu

- w przypadku xo odcięcie dużych wartości XGK

Aplikacje tego odwzorowania dla układów 1942, 1965- strefa 5, 1992 przedstawia tabela nr 3.

Dla układu UTM aplikacja odwzorowania Gaussa-Krügera jest analogiczna jak w przypadku układu 1942 z przedziałem na pasy 6º. Różnica polega jednak na odmienności przyjętych elipsoid odniesienia i skali mo a także na sposobach konstruowania współrzędnych pełnych.

Tabela.3. Aplikacje odwzorowania Gaussa-Krűgera

APLIKACJE ODWZOROWANIA GAUSSA-KRŰGERA

Wzory ogólne: Xukład aplikacyjny=m0*xGK+x0

Yukład aplikacyjny=m0*yGK+y0

UKŁAD

STREFA

ELIPSOIDA

PARAMETRY STAŁE

1942/15(6)

1942/21(6)

1942/15(3)

1942/18(3)

1942/21(3)

1942/24(3)

1965-STREFA5

KRASSOWSKIEGO

1,0

0,999983

-4700000

3500000

4500000

5500000

6500000

7500000

8500000

237000

1992

2000/15

2000/18

2000/21

2000/24

UTM/33

UTM/34

GRS-80 (WGS-84)

0,9993

0,999923

0,9996

-5300000

500000

5500000

6500000

7500000

8500000

500000*)

*) */33 */34 oznaczają strefy Polskie układu UTM według numerów słupów podziałowych międzynarodowej mapy świata; w nomenklaturze wojskowej (NATO-wskiej) i nawigacyjnej, zamiast współrzędnych pełnych w układzie UTM stosuje się specjalną systematykę alfanumeryczną określania pozycji. W aplikacjach dla potrzeb cywilnych w Polsce stosuje się również współrzędne pełne konstruowane analogicznie jak w układach strefowych 1942/15(6), 1942/21(6) . Podobna zasadę przyjęto w programach aplikacyjnych TRANSPOL i GEONET_unitrans .

Przed II Wojną Światową w Polsce używane było odwzorowanie Gaussa-Krügera w pasach dwustopniowych. Tworzyły one układy:

1 poznański o długości geodezyjnej południka osiowego 17°,

2 łęczycki o długości geodezyjnej południka osiowego 19°,

3 warszawski o długości geodezyjnej południka osiowego 21°,

4 lubelski o długości geodezyjnej południka osiowego 23°,

5 wileński o długości geodezyjnej południka osiowego 25°.

Powierzchnią odniesienia była elipsoida Bessela styczna do powierzchni geoidy w punkcie Borowa Góra.

Odwzorowanie Gaussa-Krügera do prac kartograficznych stosowane nie było. Władze wojskowe do odwzorowań dla celów wojskowych stosowały odwzorowanie quasi-stereograficzne Roussilhea.

Po II wojnie dla robót geodezyjnych oraz dla opracowania mapy gospodarczej kraju przyjęto odwzorowanie Gaussa-Krügera z podziałem obszaru państwa na pasy trzystopniowe z założeniem, że skala liniowa w każdym południku osiowym wynosiła 0.999935.

Pasy trzystopniowe tworzyły układy:

1 układ szczeciński o długości geodezyjnej południka osiowego 15°,

2 układ bydgoski o długości geodezyjnej południka osiowego 18°,

3 układ warszawski o długości geodezyjnej południka osiowego 21°,

4 układ białostocki o długości geodezyjnej południka osiowego 24°.

Powierzchnią odniesienia jest elipsoida Krassowskiego styczna do powierzchni geoidy w punkcie Pułkowo.

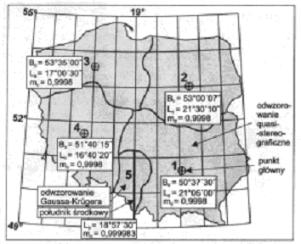
Rys. 10. Podział układu „1965” na strefy

3.Odwzorowanie quasi-stereograficzne

Odwzorowanie quasi-stereograficzne WIG (Wojskowego Instytutu Geograficznego) jest równokątnym, azymutalnym odwzorowaniem powierzchni elipsoidy obrotowej na płaszczyznę. Odpowiada ono stereograficznemu odwzorowaniu kuli , w którym występują zniekształcenia kątów.

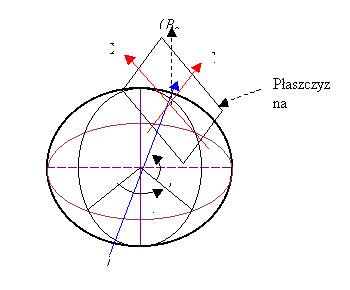
Rys. 11. Punkt główny element lokacyjny odwzorowania quasi-stereograficznego

W odwzorowaniu quasi-stereograficznym należy określić sferę styczną do płaszczyzny elipsoidy w punkcie głównym, () który jest przyłożeniem płaszczyny odwzorowania zwanym również elementem lokacyjnym. Promień Rs jest równy średniemu promieniowi krzywizny elipsoidy w tym punkcie głównym. Od punktu głównego do danego punktu B rozciągamy dowolny łuk południka środkowego mierzonego na elipsoidzie. Następnie stosując rzut stereograficzny rzutujemy ze sfery na płaszczyznę ten łuk.(środek rzutów leży w odległości od punktu głównego).

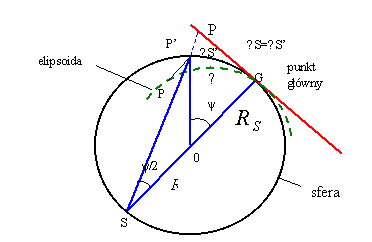
Rys. 12. Zasada odwzorowania południka środkowego

Jest to zaledwie przekształcenie łuku południka środkowego (przechodzącego przez punkt główny) w odciętą osi ox układu kartezjańskiego. Aby jednak odwzorowanie to było w pełni zrealizowane należy spełnić jedynie warunek wiernokątności. Odwzorowanie łuku południka środkowego wyraża zależność następującej postaci:

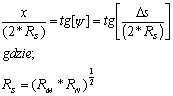
; (2.13) ;

;

gdzie:

promienie krzywizny w punkcie głównym:

- średni,

- w przekroju południkowym

- w przekroju poprzecznym, tj. pierwszego wertykału

a, e - półoś równika i mimośród elipsoidy

Przy założeniu, że istnieje równolegle odwzorowanie Gaussa-Krügera z południkiem środkowym Lo przechodzącym przez punkt główny, łuk wyraża się w postaci różnicy odciętych

gdzie:

s oznacza długość łuku południka od równika do punktu głównego. Wierniokątność obu odwzorowań sprawia, że powyższe zależności uogólniają się do postaci zespolonej, wyrażającej wzajemne przekształcenie płaszczyzn obu odwzorowań co przedstawia rysunek poniżej

W=tg(w) (2.16)

gdzie:

w = (u, v) , u = (x_GK- s_o) / (2× R_S) , v = y_GK / (2× R_S)

W = (U, V) , U = x / (2× R_{S )}, V = y / (2× R_S),

gdzie:

tg oznacza funkcję tangensa zespolonego;

x_GK, x_GK- współrzędne punktu w odwzorowaniu Gaussa- Krügera,

x, y - współrzędne w odwzorowaniu quasi-stereograficznym (środek układu pokrywa się z odwzorowanym punktem głównym). Z powyższych zależności wynika, że znając wzory odwzorowania Gaussa-Krügera możemy zrealizować odwzorowanie quasi-stereograficzne, (x_GK, y_GK) Þ (x, y₎, poprzez zależność W=tg(w) Dla konkretnej aplikacji uwzględniamy ponadto: przyjętą skalę podobieństwa m₀, mnożąc przez nią współrzędne x, y oraz parametry przesunięcia (X₀, Y₀₎:

X = m₀ · x + X₀) Y = m₀ · y + Y₀,

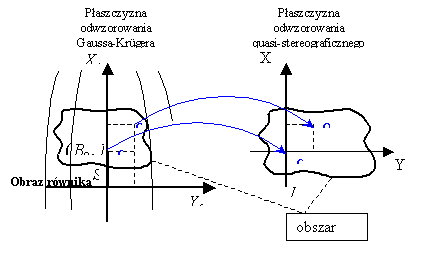
Rys. 13 Ilustracja przekształcenia pomiędzy płaszczyznami odwzorowawczymi

Z zależności W=tg(w) wynika zespolona zależność odwrotna, która ma postać:

w=arctg (W), (2.19)

która definiuje odwrotne odwzorowanie quasi-stereograficzne w stosunku do odwzorowania Gaussa-Krügera.

Odwzorowanie quasi-stereograficzne jest szczególnie przydatne do przedstawiania obszarów, których granice mają kształt regularny, zbliżony do okręgu leżących w szerokościach umiarkowanych. Punkt główny odwzorowania powinien znajdować się w pobliżu punktu środkowego odwzorowywanego obszaru. Południk przechodzący przez punkt główny nazywany jest południkiem środkowym. Południk środkowy odwzorowuje się jako odcinek linii prostej.

Odwzorowanie tego typu było stosowane na mapach wojskowych w Polsce przed II Wojną Światową. Jest to odwzorowanie elipsoidy na płaszczyznę najlepiej pasuje do obszarów zbliżonych kształtem do kwadratu. W Polsce po wojnie zastosowano tego typu odwzorowanie przy tworzeniu układu współrzędnych GUGIK 80. Układ ten wprowadzono w celu opracowania map w skalach 1:25 000 i mniejszych pokrywających cały obszar kraju. W odwzorowaniu punktem głównym jest punkt o współrzędnych B = 52º 1O’,

L = 19° 10’.

Przykładowe dane do aplikacji w układzie „1965” oraz „GUGIK-80” przedstawione są w poniższej tabeli.

STREFA 1 º 37’30’’ =21º05’00’’ =0,9998

=5467000,000m

= 4637000,000m

= 6382390,1649837m

= 5610467,5770417m

STREFA 2 º 00’07’’ =21º30’10’’ =0,9998

=5806000,000m

= 4603000,000m

= 6384119,4273046m

= 5874939,8741150m

STREFA 3 º 35’00’’ =17º00’30’’ =0,9998

=5999000,000m

= 3501000,000m

= 6384536,7935655m

= 5939644,7701117m

STREFA 4º 40’15’’ =16º40’20’’ =0,9998

=5627000,000m

= 43703000,000m

= 6383155,1651299m

= 5726819,6678288m

UKŁAD „ GUGIK-80’’ (parametry odwzorowania quasi-stereograficznego)

º 10’00’’ =19º10’00’’ =0,9997142857

=50000,000m

= 50000,000m

= 6383515,6754446 m

= 5781989,9020447m

gdzie:

- współrzędne geodezyjne punktu głównego,

- współrzędne płaskie punktu głównego,

- średni promień krzywizny powierzchni elipsoidy w punkcie głównym,

- długość łuku południka elipsoidy od równika do punktu głównego strefy,

- skala długości w punkcie głównym.

Uwaga dotycząca układu GUGiK-80: przy faktycznej realizacji układu dla map topograficznych w skalach 1:100000 dokonano dodatkowej (zamierzonej) translacji układu o kilkadziesiąt metrów. Dokładne wielkości składowych tej translacji nie są jednak odnotowane w dostępnych zasobach archiwalnych.

Góra strony