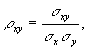Błąd kierunkowy

Wprowadzenie

W wielu rozważaniach teoretycznych, jak i w nawigacyjnych zastosowaniach praktycznych zachodzi potrzeba oceny dokładności obiektów liniowych na podstawie informacji o dokładności ich poszczególnych punktów. Na podstawie znajomości (pomiarów) wektorów losowych obliczamy parametry skalarne, jako składowe tych wektorów. Przykładem jest obliczanie odległości pomiędzy dwoma punktami, których współrzędne (dwu- lub więcej wymiarowe) określone są na podstawie pomiarów. Podobną sytuację mamy również wtedy, gdy na podstawie zmierzonych współrzędnych pozycji określamy położenie przestrzenne obiektów liniowych – izobat, krawędzi nabrzeża lub toru wodnego, linii ograniczających akwen, odległość do niebezpieczeństwa itd. W takich sytuacjach powinniśmy posługiwać się błędem kierunkowym, a nie średnim błędem kołowym.

Zależność określająca błąd kierunkowy (w kierunku wyznaczonym przez kąt a, oś X’) jest następujący:

Prawdopodobieństwo odpowiadające błędowi kierunkowemu jest równe prawdopodobieństwu błędu średniego (P = 0,683). Interpretację geometryczną błędu kierunkowego ilustruje poniższy rysunek.

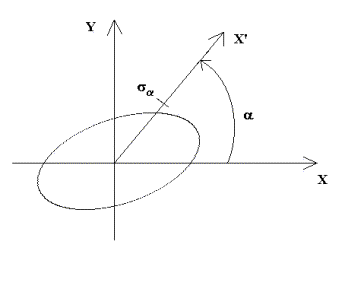
Błąd średni pozycji M wyraża się równoważnymi wzorem:

Pomiędzy średnim błędem kołowym, półosiami średniej elipsy błędów oraz błędem kierunkowym zachodzą następujące nierówności:

Zadanie:

Obliczyć i wykreślić błąd średni pozycji oraz błąd kierunkowy w funkcji zmian kąta a w zakresie zmienności od 0-360°

Zakładając, iż określamy pozycję w pewnym systemie nawigacyjnym dla którego:

s_x=100 [m]

sy=25 [m]

s_xy=1600 [m²]

Współczynnik korelacji obliczamy za formułą