Cel: Przenoszenie współrzędnych na powierzchni elipsoidy obrotowej

Opis:

Klasyczny problem obliczania współrzędnych na powierzchni elipsoidy obrotowej oraz azymutów i długości linii geodezyjnych nosi nazwę przenoszenia współrzędnych. Wyróżniamy dwa rodzaje problemu: tzw. zadanie wprost i zadania odwrotne.

Zdanie 1 – (zadanie wprost) polega na obliczeniu współrzędnych geodezyjnych B₂,L₂ punktu P₂ i azymutu linii geodezyjnej gdy dane są współrzędne punktu P₁ B₁,L₁, długość linii geodezyjnej s oraz azymut A pod jakim linia geodezyjna wychodzi z punku P.

Zadanie 2 – (zadanie odwrotne) dotyczy obliczenie długości linii geodezyjnej s łączącej na powierzchni elipsoidy dwa punkty o znanych współrzędnych P₁ i P₂ oraz obliczenia azymutów linii geodezyjnej (wprost i odwrotnie)

Przykładowa metoda obliczeń:

Spośród kilku metod obliczeń zaprezentowana zostanie metoda średniej szerokości Gaussa-zadanie wprost (Rys.1.) Kolejność obliczeń wykonujemy zgodnie z algorytmem (Rys.2.), gdzie B=j, L=l wg oznaczeń geodezyjnych. Obliczenia przenoszenia współrzędnych muszą być dokonane z przyjętą minimalną dokładnością (tab.1). Warunek ten wymaga dokonania obliczeń iteracyjnych. Załóżmy, iż w prezentowanym przykładzie warunek zostanie spełniony w drugim przybliżeniu.

Tab.1. Wymagania dokładnościowe:

•30-100 km: współrzędnych ±0.0001”, azymutu ±0.001”

•Do 1000 km: współrzędnych ±0.001”, azymutu ±0.01”

•Do 20 000 km: współrzędnych ±0.003”, azymutu ±0.03”

•

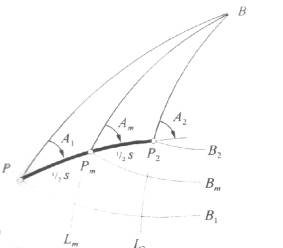
Rys.1. Metoda średniej szerokości Gaussa

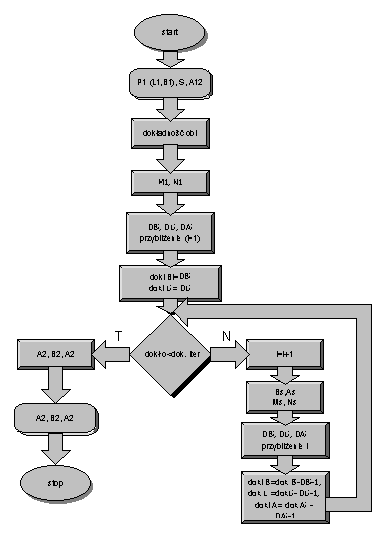
Rys.1. Algorytm obliczeń w metodzie średniej szerokości Gaussa

Poszczególne wzory zamieszczono poniżej:

Wartości poprawek obliczane są w sposób iteracyjny

Pierwsze przybliżenie

, gdzie

, gdzie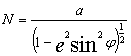

gdzie:

r”=206264.8062 - radian wyrażony w sekundach

t²=tg²j_s

Drugie przybliżenie otrzymujemy z wzorów

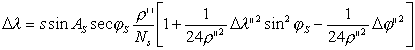
Przykładowe zadanie:

Elipsoida WGS-84

a	6378137
e^2	0.006694438
e’^2	0.0673949674227

Dane wejściowe

A=315^o

S=200000

Wynik obliczenia

A2=134.41^o