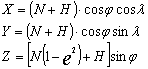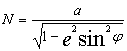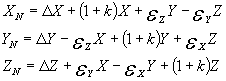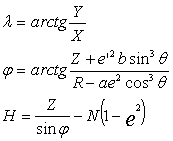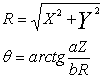Cel: Transformacja współrzędnych metodą 7-parametrową
Opis:
W praktyce nawigacyjnej często zachodzi konieczność wyrażenia współrzędnych pozycji w różnych układach współrzędnych. Dlatego też, każdy z nawigatorów powinien mieć świadomość relacji zachodzących pomiędzy tymi współrzędnymi. Równie często nieodzowne jest dokonanie transformacji współrzędnych pomiędzy układami odniesienia. Jedną z metod transformacji jest transformacja 7-parametrowa (Rys.1.)
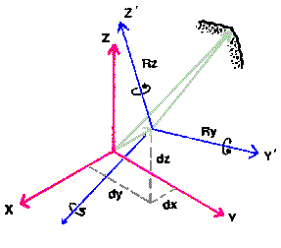
Rys. 1. Transformacja współrzędnych metodą 7-parametrową
Kolejność obliczeń:
1. Korzystając z poniższych zależności przekształcamy współrzędne B,L na X, Y, Z
|
|
|
gdzie:
|
|
|
2. Obliczamy XN ,YN, ZN z zależności:
|
|
|
3. Obliczamy
![]() korzystając z
zależności
korzystając z
zależności
|
|
|
gdzie:
|
|
|
Zadanie do wykonania:
Dokonaj transformacji współrzędnych pozycji WGS-84 do układu ED 50:
Parametry transformacji podane są w poniższej tabeli.
Parametry elipsoidy WGS-84:
|
a |
6378137 m |
|
e2 |
0,00669438 |
|
e’2 |
0,006739497 |
Parametry elipsoidy ED 50:
|
a |
6378388 |
|
b |
6356911,95 |
|
e2 |
0,006722669 |
|
e’2 |
0,006768169 |
Kwadrat drugiego mimośrodu wynosi 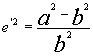
Tab. 1 Parametry transformacji wybranych układów odniesienia do układu WGS-84
|
Układ |
Krassowskiego’42 |
European
1950 |
WGS-72 |
|
ΔX [m] |
-33,4297 |
87 |
0 |
|
ΔY[m] |
146,5746 |
96 |
0 |
|
ΔZ[m] |
76,2865 |
120 |
-4,5 |
|
ex[rad] |
-1,73889*10-6 |
0 |
0 |
|
ey[rad] |
-2,56146*10-6 |
0 |
0 |
|
ez[rad] |
4,0896*10-6 |
0 |
-2,685868*10-6 |
|
k |
0,8407720*10-6 |
0 |
2,263*10-7 |
Zadanie przykładowe:
Pozycja w układzie odniesienia WGS 84
BWGS84=54o40’54.45” N
LWGS84=014o15’34.76’’ E
obliczenia pośrednie
|
X |
3 581 691,711 |
|
Y |
910 276,364 |
|
Z |
5 180 985,172 |
|
Xnew |
3 581 778,711 |
|
Ynew |
910 372,364 |
|
Znew |
5 181 105,172 |
Pozycja po transformacji
BED50 =54o40’56.64” N
LED50 =014o15’38.76” E