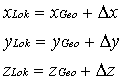Algorytmy transformacji współrzędnych

Ogólne zasady transformacji współrzędnych

Bezpośrednia metoda przeliczania współrzędnych

Metoda Bowringa

Transformacja współrzędnych kartezjańskich

Transformacja za pomocą wzorów Mołodienskiego

Podsumowanie

Algorytmy transformacji współrzędnych

Zagadnienie transformowania współrzędnych pomiędzy różnymi układami odniesienia nabrało szczególnego znaczenia wraz z rozpowszechnianiem satelitarnego systemu nawigacyjnego. Problem ten staje się istotny również przy wyznaczaniu granic na morzu, a w związku z tym pojawiania się kontrowersji dotyczących ewentualnych naruszeń określonych akwenów, np. rybołówczych czy terytorialnych.

Dawniej pozycję wyznaczano metodami graficznymi w oparciu o znaki nawigacyjne zaznaczone na tej samej mapie. W związku z tym problem zmiany układu odniesienia mógł wystąpić tylko w momencie zmiany mapy. Kiedy pojawiły się odbiorniki systemu TRANSIT okazało się, że znaki nawigacyjne w stosunku, do których dokonywano pomiarów nie są zaznaczone na mapie, a wyznaczanie pozycji na ich podstawie dokonuje się analitycznie w komputerze. Dopiero na przełomie lat 80-tych pojawiły się na mapach brytyjskich informacje o stosowanym układzie odniesienia. Rozpoczęto wtedy również zamieszczanie informacji o wartościach poprawek, jakie należy uwzględnić przy nanoszeniu na taką mapę pozycji określonej systemem satelitarnym.

We współczesnej praktyce powszechnie stosowanym w systemach GPS jest układ odniesienia WGS 84. Spotykamy się jednak ze stosowaniem różnych układów odniesienia dla danych mapy. W związku z tym należy oczekiwać, że współrzędne tych samych punktów nie będą wyrażały się takimi samymi wartościami. Zatem stosowanie różnych układów odniesienia wywołuje pewne błędy, które w danym miejscu mają charakter błędów systematycznych, a zależą od różnic w rozmiarach i kształcie stosowanych elipsoid oraz wzajemnego usytuowania tychże elipsoid. W rezultacie w procesie obliczeń należy uwzględnić procedury transformowania współrzędnych do wspólnego układu odniesienia, przy czym wspólny może być jeden ze stosowanych układów lub zupełnie inny.

Zatem różnice współrzędnych wywołane różnymi układami odniesienia są porównywalne ze zwykłymi błędami określania pozycji. Tak więc problem transformacji współrzędnych jest powszechnie znany i spotykany zarówno przy pomiarach satelitarnych jak i przy wykorzystaniu systemów naziemnych.

Ogólne zasady transformacji współrzędnych

Na rysunku poniżej przedstawiony jest schemat ilustrujący różnice między pojęciami układ odniesienia i układ współrzędnych. Kolumny oznaczają na nim różne układy odniesienia, natomiast wiersze różne sposoby tworzenia układu współrzędnych. W nawigacji najczęściej mamy do czynienia z przypadkiem współrzędnych φ_A , λ_A lub φ_B , λ_B .Dla nawigatora oznacza to, że niezależnie, jaką mapą się on posługuje to pozycja będzie opisana tymi właśnie wartościami. Zatem warto wspomnieć o tym, że nie wolno przenosić pozycji z mapy na mapę w oparciu o współrzędne. Może to być dopuszczalne tylko i wyłącznie, gdy jesteśmy pewni, że obie mapy zostały wykonane w oparciu o ten sam układ odniesienia. W dzisiejszych czasach nowej technologii nie trzeba się martwić o tego typu sprawy, gdyż większość map wykonana jest w oparciu o układ WGS 84, jednak na niektórych obszarach na świecie istnieją jeszcze mapy oparte o lokalny, czy też regionalny układ odniesienia.

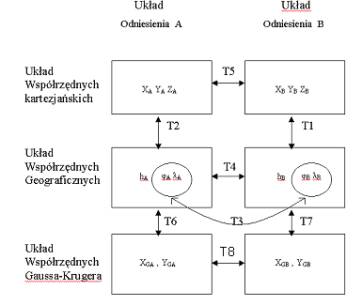
Rys. Schemat zależności pomiędzy różnymi układami współrzędnych i różnymi układami odniesienia

Strzałki opisane literami T1.....T8. Oznaczają transformację współrzędnych.

Transformacje to metody zamiany jednych współrzędnych na inne, np. geodezyjne na płaskie Gaussa – Krugera. Transformowanie T6 oraz T7 jest jednym z najpowszechniejszych. Strzałki poziome na schemacie oznaczają transformacje współrzędnych tego samego rodzaju pomiędzy różnymi układami odniesienia. Najważniejsze transformacje to T3 i T4 pomiędzy współrzędnymi geograficznymi wyrażanymi w różnych układach odniesienia.

Warto tutaj również przytoczyć schemat przedstawiający ścieżki przejść transformacyjnych pomiędzy różnymi układami stosowanymi w obszarze Polski. Schemat wskazuje przede wszystkim, że aby przeliczyć współrzędne z układów dawnych (jako odwzorowań elipsoidy Krasowskiego) do układów nowych (powstałych z elipsoidy GRS-80 lub WGS-84) lub odwrotnie, należy przejść przez współrzędne globalne obu systemów elipsoidalnych, tj. współrzędne kartezjańskie - geocentryczne XYZ lub geodezyjne BLH. Nie ma takiej potrzeby, jeśli problem przeliczeniowy dotyczy układów kartograficznych tej samej elipsoidy.

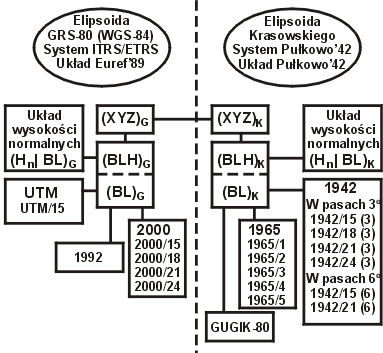
Rys. Schemat bezpośrednich przejść transformacyjnych pomiędzy układami współrzędnych

Przeliczenie współrzędnych pomiędzy dwoma dowolnymi układami wymienionymi na schemacie powinno być w zasadzie złożeniem przekształceń elementarnych, które wskazują linie łączące. Poprzez analityczne lub numeryczne złożenie operacji można oczywiście uzyskać wzory innych przejść transformacyjnych. Przejście pomiędzy elipsoidami może być realizowane poprzez współrzędne kartezjańskie X,Y,Z (metoda podstawowa), jak też poprzez współrzędne geodezyjne B,L,H (po uwzględnieniu matematycznych zależności pomiędzy B,L,H i X,Y,Z).

Transformacja współrzędnych dzieli się na transformacje 3-parametrową oraz 7-parametrową. Transformacja siedmio-parametrowa jest bardziej ścisłą metodą, gdzie parametry muszą wskazywać na przemianę miejscowych współrzędnych danego układu odniesienia do współrzędnych układu WGS 84.

Dla wielu typowych aplikacji GIS-u można zmienić znak każdego z siedmiu parametrów, by otrzymać odwrotność, choć nie zawsze ta technika jest dokładna.

Parametrami transformacji są:

a) Delta X – przesunięcie względem osi X. Wartość ta musi być podawana w metrach a kierunek translacji podawany jest przez znak wartości.

b) Delta Y – przesunięcie względem Y. Wartość ta musi być podawana w metrach a kierunek translacji podawany jest przez znak wartości.

c) Delta Z - przesunięcie względem Z. Wartość ta musi być podawana w metrach a kierunek translacji podawany jest przez znak wartości.

d) Rotacja X – rotacja wokół osi X. Wartość ta jest podawana w sekundach, a kierunek rotacji jest wskazany przez znak wartości.

e) Rotacja Y – rotacja wokół osi Y. Wartość ta jest podawana w sekundach, a kierunek rotacji jest wskazany przez znak wartości.

f) Rotacja Z – rotacja wokół osi Z. Wartość ta jest podawana w sekundach, a kierunek rotacji jest wskazany przez znak wartości.

g) Skala – współczynnik skalowania. Wartość podawana jest w częściach na milion(ppm) i jest różnicą aktualnego współczynnika skalowania i jednostek.

Na rysunkach poniższych przedstawione są parametry transformacji zarówno 3-parametrowej (a) jak i 7-parametrowej(b).

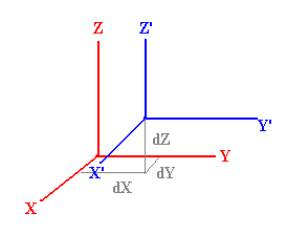
Rys. - parametry transformacji 3-parametrowej

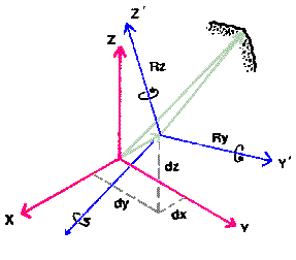
Rys. parametry transformacji 7-parametrowej

Bezpośrednia metoda przeliczania współrzędnych

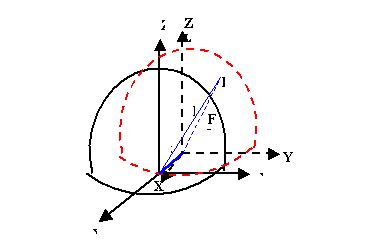
Metoda bezpośrednia jest jedną z najbardziej popularnych metod transformacji współrzędnych i polega na zamianie współrzędnych geograficznych punktu P (φ, λ, h) na współrzędne geograficzne w innym układzie odniesienia (środek układu znajduje się tutaj w środku elipsoidy, oś z pokrywa się z osią obrotu elipsoidy, natomiast płaszczyzna X, Y, Z płaszczyzną równika.

Współrzędne prostokątne X, Y, Z punktu P wyrażone w geocentrycznym układzie odniesienia, przy przeliczeniu ich na współrzędne prostokątne w układzie lokalnym X_L, Y_L, Z_L

Rys. Przesunięcie układu lokalnego i globalnego o wektor r_o

będą różniły się o wartość poprawek dX, dY, dZ, opisujących wektor r_o. Układu współrzędnych prostokątnych przestrzennych nie stosujemy w celu opisywania pozycji w nawigacji, jednak aby wykorzystać tą metodę musimy zamienić współrzędne geograficzne punktu wyrażone w geocentrycznym układzie odniesienia współrzędnych φ, λ, h na przestrzenne współrzędne prostokątne X, Y, Z w tym samym układzie.

W tym celu należy skorzystać z poniższych zależności:

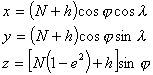
gdzie:

X, Y, Z –współrzędne prostokątne przestrzenne punktu P

N – promień przekroju pierwszego wertykału,

e² – kwadrat pierwszego mimośrodu

j, l, h – współrzędne geograficzne punktu P

Następnym krokiem przy transformacji jest dokonanie translacji o w/w wektor r₀ (dX, dY, dZ), dzięki czemu otrzymamy współrzędne prostokątne przestrzenne X_L, Y_L, Z_L w innym układzie. Wzory te będą wyrażone następująco:

Jednakże wartości wektora r₀ nie są identyczne, a wręcz przeciwnie różnią się dla każdego układu odniesienia, co przedstawia poniższa tabela:

Tab. Wartości poprawek dla niektórych układów odniesienia w stosunku do WGS 72

Nazwa układu odniesienia	Wartości niektórych przestrzennych współrzędnych prostokątnych w stosunku do układu WGS 72
	Dx [m]	Dy [m]	Dz [m]
Australijski (AND)	-122	-41	146
Europejski (ED-50)	-84	-103	-127
Północnoamerykański (NAD 27)	-22	157	176
Południowoamerykański ( SAD 69)	-77	3	45

Współrzędne prostokątne przestrzenne układu lokalnego można zamienić na współrzędne geograficzne w tym układzie odniesienia. W tym celu posłużymy się następującymi wzorami:

Na początku wyznaczymy długość:

a następnie pierwsze przybliżenie szerokości φ_o:

Następnie obliczamy kolejne przybliżenia szerokości φ:

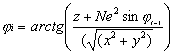
oraz wysokości H, którą możemy obliczyć za pomocą wzorów:

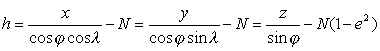
lub:

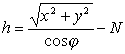
a także

Obliczenia przybliżeń φ_i i H_i zakończą się po przekroczeniu założonej dokładności ε , np. ε = 10^-7 rad, a więc gdy zachodzi nierówność:

oraz

gdzie:

a – duża półoś elipsy

Innym sposobem transformacji współrzędnych przestrzennych ortokartezjańskich jest tak zwana metoda numeryczna, czyli przeliczanie x, y, z na B, L ,H dla dowolnych wartości H. „Numeryczność” tej metody polega na tym, że mnożniki Lagrange’a tworzą równanie czwartego stopnia, które rozwiązywane jest numerycznie.

W nawigacji morskiej mamy do czynienia z problemem transformacji współrzędnych punktów, których odległość od powierzchni elipsoidy waha się w granicach od –100 do +100 metrów.

Metodę numeryczną będę rozpatrywał dokładnie w punktach, przytaczając kilka przypadków, zaczynając od najbardziej błahych. Przyjmijmy, że P (x_o, y_o, z_o) jest ustalonym punktem w układzie współrzędnych ortokartezjańskich, którego początek pokrywa się ze środkiem elipsoidy o półosiach a i b.

Na początku rozpatrzmy kilka łatwych przykładów:

1. Punkt P ma współrzędne (0,0,0). Zatem będzie pokrywał się on z początkiem układu współrzędnych i posiada dwa równoprawne rzuty ortogonalne na powierzchnię elipsoidy, tzw. Bieguny.

2. Punkt P ma współrzędne(x_o, 0,0) zatem leży na osi Ox, a jego współrzędne geodezyjne są równe:

B = 0º

L = 0^o, gdy x_o > 0

L = 180º , gdy x_o < 0

3. Punkt P ma współrzędne (0, y₀ ,0). Leży on wtedy na osi Oy, a jego współrzędne geodezyjne wynoszą:

B = 0º

L = 90º , gdy y_o > 0

L = -90º , gdy y_o < 0

4. Punkt P ma współrzędne (0,0, z_o), zatem leży na płaszczyźnie osi Oz:

B = 90º , gdy z_o > 0

B = -90º , gdy z_o < 0

L - jest nieokreślona

5. Punkt P ma współrzędne (x_o, y_o, 0), zatem leży na płaszczyźnie Oxy.

B = 0º

6. Punkt P ma współrzędne (x_o, 0, z_o) i leży na płaszczyźnie Oxz:

L = 0^o, gdy x_o > 0

L = 180º , gdy x_o < 0

B oraz H będziemy obliczali tak jak w n/w punkcie 8.

7. Punkt P ma współrzędne (0, y_o, z_o), więc leży na płaszczyźnie Oyz:

L = 90º , gdy y_o > 0

L = -90º , gdy y_o < 0

B oraz H będziemy obliczali tak jak w n/w punkcie 8.

8. Punkt P ma współrzędne (x_o, y_o, z_o) , wszystkie różne od zera. W tym przypadku będą rozpatrywane trzy różne sytuacje:

a) punkt P leży na powierzchni elipsoidy, czyli jest punktem tzw. Elipsoidy południkowej, zatem H=0, a pozostałe współrzędne są równe:

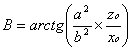
gdzie:

b) punkt P jest punktem zewnętrznym elipsoidy, tzn. H > 0, co przedstawia poniższy rysunek:

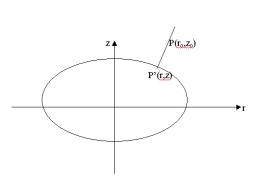
Rys. przedstawienie punku zewnętrznego na elipsoidzie

c) punkt P leży we wnętrzu elipsoidy, czyli H < 0

Współrzędna L będzie obliczana w przypadkach b i c tak jak w przypadku 8a, natomiast trudniejszą sprawą jest tutaj obliczenie współrzędnych B i H.

Aby obliczyć szerokość geodezyjną B potrzebujemy najpierw rozpatrzyć elipsoidę południkową o równaniu:

zakładamy, że a > b > 0, zatem musimy znaleźć taki punkt P’ (r, z) na elipsie E, dla którego spełniony będzie warunek:

czyli minimalnej odległości od punktu P do P’ na elipsoidzie ziemskiej.

Problem ten będziemy rozwiązywać za pomocą mnożników Lagrange’a. Potrzebne nam będzie do tego określenie dwóch następujących funkcji:

stąd otrzymujemy:

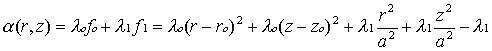
gdzie:

λ_o , λ₁ – mnożniki Lagrange’a

Za pomocą twierdzenia Fermata wyznaczymy ekstremum w/w wzoru, zatem musi być spełniony warunek istnienia ekstremum dwóch zmiennych:

jednak warunek ten będzie spełniony gdy zajdą poniższe równości:

Nie możemy jednak przyjąć zależności, że r = z =0, dlatego λ_o0.

Można założyć, że λ_o=1, wtedy w/w zależności przyjmą postać:

Z tych zależności otrzymamy, że współrzędne punktu P’ na elipsie E w funkcji λ₁ są równe:

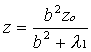
Podstawiając to do wzoru /11/ otrzymamy postać funkcji zmiennej λ₁:

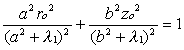
po przekształceniu otrzymamy następujące równanie czwartego stopnia względem λ₁:

gdzie:

Powyższe równanie możemy rozwiązać numerycznie z dowolną dokładnością. Otrzymamy wtedy max. cztery różne wartości λ₁ , które po podstawieniu do wzorów /21/ i /22/ dadzą taką samą ilość wartości r i z.

Z kolei dla tych par musimy znaleźć minimalną wartość funkcji f_o wzór /13/.

Wysokość elipsoidalną obliczamy jako pierwiastek z minimalnej wartości f_o, tj.

Ponieważ współrzędne punktu P’ i jego wysokość jest równa zero(H’=0), to szerokość geodezyjna tego punktu, a co za tym idzie także punkt P, będzie równa:

Pozostałe współrzędne obliczmy według wcześniej podanych wzorów, w zależności od tego którego przypadku dotyczą.

W nawigacji morskiej mamy zazwyczaj do czynienia z przypadkami 8b i 8c, zatem wykorzystywać będziemy wzory /8/, /24/, /25/.

Przedstawiona wyżej metoda jest metodą ogólną i może być wykorzystywana do transformacji punktów o dowolnej odległości od elipsoidy.

Trzecim sposobem zamiany współrzędnych przestrzennych na geodezyjne, jest tzw. metoda przybliżona. W metodzie tej podam zależności które zostały wyprowadzone w oparciu o współrzędne punktu C (rys.) będącego środkiem okręgu stycznego do elipsy południkowej w punkcie P’.

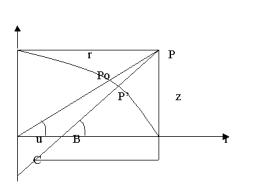
Rys. Współrzędne punktów na elipsoidzie

Współrzędne tego punktu wynoszą:

gdzie: u – jest to szerokość zredukowana punktu P

Z rysunku widać, że (przy założeniu, że znamy współrzędne punktu C):

Jako, że współrzędne punktu C są wartościami przybliżonymi, powyższy wzór również taki jest. Błąd szerokości B zależny jest od wysokości punktu H. Jednak dla wysokości spotykanych w nawigacji morskiej błąd szerokości obliczony powyższym wzorem nie przekracza 10^-7 sekundy kątowej.

Inną przybliżoną zależność na obliczanie szerokości geodezyjnej punktu można uzyskać za znanego związku pomiędzy szerokością geodezyjną i szerokością geocentryczną punktu leżącego na elipsoidzie:

gdzie: ψ- szerokość geocentryczna

Z rysunku możemy zapisać pewną zależność:

Przekształcając powyższe wzory otrzymujemy:

zależność ta jest prawdziwa dla punktów leżących na elipsoidzie, zatem H = 0.

Zatem można to przedstawić w innej postaci:

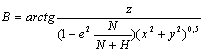
Transformacja przestrzennych współrzędnych kartezjańskich na współrzędne geodezyjne możliwa jest metodą iteracyjną, przybliżoną a także numeryczną.

Ta ostatnia metoda zazwyczaj nie jest używana w praktyce ze względu na równanie czwartego stopnia. Wzory iteracyjne zapewniają wymaganą dokładność obliczeń.

Najkorzystniejsze dla celów nawigacyjnych są zależności przybliżone.

Metoda Bowringa

Metoda ta polega na transformacji współrzędnych geograficznych (geodezyjnych) na nowe współrzędne geograficzne(geodezyjne), przy pomocy współrzędnych ortokartezjańskich.

Transformacja odbywa się w trzech kolejnych etapach:

1) Transformacja współrzędnych geograficznych (geodezyjnych) j, l i H na ortokartezjańskie X, Y, Z:

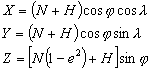
gdzie:

a – duża półoś elipsoidy ziemskiej

b – mała półoś elipsoidy

e – pierwszy mimośród elipsoidy ziemskiej

N – promień pierwszego wertykału

DX, DY, DZ – przyrost współrzędnych względem WGS-84, a pozostałymi układami

e_X, e_Y, e_Z – skręcenie względem osi x, y, z

2) Transformacja ze współrzędnych ortokartezjańskich X, Y, Z na nowe ortokartezjańskie X_NEW, Y_NEW, Z_NEW dla układu odniesienia, na który przeliczamy:

gdzie:

DX, DY, DZ – przyrost współrzędnych względem WGS-84, a pozostałymi układami

e_X, e_Y, e_Z – skręcenie względem osi x, y, z

3) Przeliczanie ze współrzędnych ortokartezjańskich X_NEW, Y_NEW, Z_NEW na geograficzne (geodezyjne) j_NEW, l_NEW, H_NEW (do obliczeń w tej części wykorzystuje się wartości a, b, e², e’², N dla nowego układu odniesienia):

gdzie:

a – duża półoś elipsoidy ziemskiej

b – mała półoś elipsoidy

e – pierwszy mimośród elipsoidy ziemskiej

e’ – drugi mimośród elipsoidy ziemskiej

N – promień pierwszego wertykału

Transformacja współrzędnych kartezjańskich

Jest to transformacja trójwymiarowa przez podobieństwo, zdefiniowana jednoznacznie przez 7 parametrów, tj. trzy składowe przesunięcia wzajemnego środków elipsoid, trzy kąty obrotów osi jednego układu względem drugiego oraz jeden parametr zmiany skali. Zadanie to realizują wzory praktyczne (podane stałe są funkcjami siedmiu geometrycznych parametrów przekształcenia):

Przejście z elipsoidy WGS 84 na elipsoidę Krasowskiego:

(XYZ)_{w Þ} (XYZ)_k

X_K= X_W + C₁₁*X_W + C₁₂*Y_W + C₁₃*Z_W + T_X

Y_K= Y_W + C₂₁*X_W + C₂₂*Y_W + C₂₃*Z_W + T_Y

Z_K= Z_W + C₃₁*X_W + C₃₂*Y_W + C₃₃*Z_W + T_Z

gdzie:

T_X = - 33.4297 m

T_Y = + 146.5746 m

T_Z = + 76.2865 m

C₁₁ = + 0.84076440*10^-6

C₂₁ = - 4.08960650*10^-6

C₃₁ = - 0.25614618*10^-6

C₁₂ = + 4.08960694*10^-6

C₂₂ = + 0.84076292*10^-6

C₃₂ = + 1.73888682*10^-6

C₁₃ = + 0.25613907*10^-6

C₂₃ = - 1.73888787*10^-6

C₃₃ = + 0.84077125*10^-6

Przejście z elipsoidy Krasowskiego na elipsoidę WGS 84:

(XYZ)_{k Þ} (XYZ)_w

X_W= X + D₁₁*X + D₁₂*Y + D₁₃*Z

Y_W= Y + D₂₁*X + D₂₂*Y + D₂₃*Z

Z_W= Z + D₃₁*X + D₃₂*Y + D₃₃*Z

gdzie:

X = X_K – T_X

Y = Y_K – T_Y

Z = Z_K – T_Z

D₁₁ = - 0.84078048*10^-6

D₂₁ = + 4.08960007*10^-6

D₃₁ = + 0.25613864*10^-6

D₁₂ = - 4.08959962*10^-6

D₂₂ = - 0.84078196*10^-6

D₃₂ = - 1.73888494*10^-6

D₁₃ = - 0.25614575*10^-6

D₂₃ = + 1.73888389*10^-6

D₃₃ = - 0.84077363*10^-6

Transformacja za pomocą wzorów Mołodienskiego

Metoda ta jest metodą tzw. trzy parametrową, gdzie wzory będą wykorzystywane na określenie poprawek Δφ, Δλ, Δh, o które należy poprawić współrzędne pozycji (φ, λ, h), przechodząc do innego układu odniesienia.

Wzory zostały opracowane na podstawie poniższych zależności:

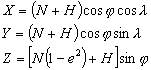
jednak przy założeniu, że oba układy odniesienia są wzajemnie równoległe, ich środki są przesunięte o wektor ΔR, a jeden z układów jest układem geocentrycznym.

Poprawki Δφ, Δλ, Δh równe są różnicom między wartością: szerokości geograficznej, długości geograficznej i wysokości w nowym układzie a wartością tej samej wielkości w dotychczasowym układzie. Przez Δa, Δe² , Δα oznaczamy przyrosty dużej półosi, kwadratu pierwszego mimiśrodu i biegunowego spłaszczenia elipsoidy.

Składowe Δx, Δy, Δz, wektora ΔR można przedstawić jako różniczki zupełne względem φ, λ, h, a, e² . Wtedy otrzymujemy następujące zależności[3]:

Pochodne cząstkowe mają postać:

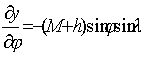
gdzie:

φ, λ, h – współrzędne pozycji w dotychczasowym układzie odniesienia

N – promień krzywizny pierwszego wertykału

M – promień krzywizny południka:

a – duża półoś elipsoidy dotychczasowego odniesienia.

Przyrost kwadratu pierwszego mimośrodu (Δe²) można wyrazić za pomocą parametru α charakteryzującego jej biegunowe spłaszczenie:

Z zależności:

e² = 2α – α²

różniczka de² jest równa:

de² = 2b/a

tym samym otrzymujemy:

uwzględniając poniższe założenie:

po odpowiednich przekształceniach powyższych równań otrzymamy zależności określające szukane wartości poprawek Δφ, Δλ, Δh, przy czym wartości poprawek dotyczących zarówno szerokości jak i długości geograficznej wyrażone są w sekundach, a wysokości w metrach:

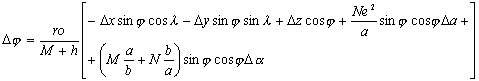
gdzie:

r – wartość radiana wyrażona w sekundach, równa 206264,806

Do celów nawigacyjnych można stosować skróconą postać wzorów Mołodieńskiego:

W powyższych wzorach przy przeliczaniu współrzędnych z układu lokalnego do geocentrycznego, wszystkie przyrosty (Δα, Δa, itp.) oznaczają różnice, które powstają w wyniku odejmowania wartości parametrów: elipsoidy lokalnej od elipsoidy WGS, zatem elipsoidy globalnej.

Pozostałe wartości to:

a - większe półosie elipsoidy lokalnej

b - mniejsza półoś elipsoidy lokalnej

α - spłaszczenie elipsoidy lokalnej

φ, λ, h – współrzędne geograficzne elipsoidy lokalnej

b/a = 1 - α

e² = 2α – α²

M, N – promienie krzywizny południka i pierwszego wertykału

Podczas przeliczania współrzędnych z układu geocentrycznego do układu lokalnego obowiązuje odwrotna zasada do wyżej przedstawionej.

Metoda oparta na wzorach Mołodieńskiego umożliwia przeliczanie współrzędnych z jednego układu odniesienia do drugiego z dokładnością 0,03” w wypadku współrzędnych geograficznych (φ, λ) oraz 0,5 m w przypadku wysokości h.

Góra strony

Podsumowanie

Transformacja współrzędnych jest jednym z zadań obliczeniowych często występujących w praktyce geodezyjnej. Polega ona na przeliczeniu współrzędnych z jednego układu na inny (najczęściej z pierwotnego na wtórny). Warunkiem przeprowadzenia poprawnej transformacji jest znajomość relacji zachodzących między współrzędnymi punktów wyrażonych w rozpatrywanych układach. Formuła (wzory) matematyczna przedstawiająca związki między współrzędnymi nazywana jest równaniem transformacyjnym. Istnieje opracowanych wiele modeli transformacji opisanych w literaturze geodezyjnej (także dostępne są specjalistyczne programy komputerowe) m.in.:

- model Bursy-Wolfa

- model Mołodienskiego

- model Mołodienskiego-Badekasa

- model Veisa

- model Wellsa-Vanicka

- model Krakiwskiego-Thomsona

Oczywistym jest, iż określona pozycja w zależności od stosowanego układu odniesienia, będzie opisana różnymi (innymi) współrzędnymi. Nawigator musi mieć pełną świadomość istnienia tego faktu. Różnice pozycji w przypadku zaniechania przez nawigatora przeliczenia współrzędnych (lub też nieuwzględnienia poprawek) mogą być znaczne i wpłynąć na bezpieczeństwo nawigacji (wg Notices to Mariners:„MAY BE SIGNIFICANT TO NAVIGATION”!)