Układy współrzędnych

Współrzędnymi nazywamy wielkości kątowe lub liniowe, wyznaczające położenie punktu na dowolnej powierzchni lub w przestrzeni w sposób względny w stosunku do przyjętych za początek układu płaszczyzn lub linii. Istnieje wiele układów współrzędnych szeroko stosowanych w różnych dziedzinach nauki i techniki

W zależności od potrzeb układy współrzędnych realizuje się na różne sposoby.

Wszystkie układy współrzędnych różnią się od siebie charakterystyką geometryczną. Dotyczy ona położenia początku układu jak również kierunków osi współrzędnych, a w przypadku układów krzywoliniowych sposobu realizacji kątów, które określają położenie punktu na określonej powierzchni.

1. Układ współrzędnych geograficznych na kuli

Układ współrzędnych geograficznych jest jednym z najstarszych układów współrzędnych, który najlepiej spisywał się na morzu. Położenie punktu opisane jest w nim przy pomocy dwóch kątów określających geocentryczny kierunek do danego punktu.

Punkt ten może być położony pod wodą, na powierzchni mórz, ponad powierzchnią Ziemi, w atmosferze albo w przestrzeni kosmicznej. Ten układ, w którym określone są szerokość geograficzna j i długość geograficzna l wymaga niewielkiej dokładności określenia położenia, rzędu dziesiątek metrów.

Należy zwrócić uwagę na fakt, że oprócz niewielkiej dokładności, w danym układzie nie występuje współrzędna wysokość punktu, przez którą rozumiemy odstęp punktu od określonej powierzchni odniesienia geoidy.

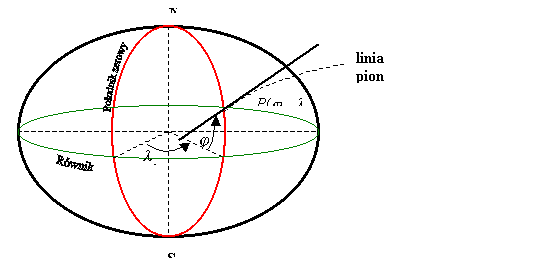
Początek układu znajduje się w środku geometrycznym kuli, a za pomocą szerokości geograficznej j i długości geograficznej l, określa się położenie punktu P na powierzchni kuli.

Rys. 1. Układ współrzędnych geograficznych na kuli.

Szerokością geograficzną punktu P nazywamy kąt j pomiędzy promieniem wodzącym tego punktu, a płaszczyzną równika. Szerokość geograficzną wyznacza się za pomocą obserwacji wysokości kątowej nad horyzontem wybranego ciała niebieskiego, posługując się tablicami astronomicznymi zawierającymi pozycje ciał niebieskich na dany rok, dzień, godzinę.

Ze względu na kulisty kształt Ziemi, każda zmiana pozycji wzdłuż linii północ-południe pociąga za sobą taką samą zmianę kątowej wysokości obserwowanego ciała niebieskiego, na przykład zmiana szerokości geograficznej o 1º powoduje zmianę kątowej wysokości obserwowanego ciała niebieskiego również o 1º.

Rozumowanie to jest nieco uproszczone, ponieważ nie uwzględnia obrotowego ruchu Ziemi i, związanego z nim, względnego ruchu ciał niebieskich. Nie zmienia to jednak podstawowej zasady, że położenie punktu na kierunku północ—południe może być określone przez pomiar kąta między płaszczyzną horyzontu a kierunkiem na ciało niebieskie.

Ta prosta zależność między wielkościami liniowymi a kątowymi w systemie współrzędnych geograficznych znalazła praktyczne zastosowanie. Już w starożytności przeprowadzono niezliczoną liczbę równoległych do siebie okręgów opasujących kulę ziemską. Najdłuższy z nich, dzielący glob na dwie równe części, nazwany został równikiem.

Szerokości geograficzne północne określają okręgi, które są położone na północ od równika. Natomiast szerokość geograficzną południową określają te, które leżą na południe od równika. Pomiaru kąta między płaszczyzną horyzontu miejsca obserwacji a Słońcem, Gwiazdą Polarną lub innym ciałem niebieskim, prowadzi do ustalenia równoleżnika miejsca obserwacji, czyli określenie jego kątowej wysokości północnej lub południowej.

W systemie współrzędnych geograficznych wprowadzonych blisko 2000 lat temu nie dokonano żadnych zmian.

Długością geograficzną punktu P nazywamy kąt dwuścienny l, zawarty pomiędzy płaszczyzną południka zerowego, a płaszczyzną południka przechodzącego przez punkt P. Długość geograficzna umożliwia określenie pozycji w kierunku wschód-zachód. Długość geograficzną punktu wyznacza przechodzący przez ten punkt, prostopadle do równoleżników, południk geograficzny. Wśród linii południkowych nie można jednak wyróżnić południka początkowego, jak dzieje się to w przypadku równoleżników względem, którego mierzono by odległości kątowe w kierunku wschód lub zachód w stopniach, minutach i sekundach. Z tego względu wybiera się południk początkowy arbitralnie. Przyjmuje się, że południk początkowy ma długość geograficzną równą 0°, wskutek czego bywa nazywany południkiem zerowym. Względem południka początkowego (zerowego) odmierzane są w mierze kątowej, wzdłuż równoleżników długości geograficzne

2. Układ współrzędnych geodezyjnych B, L

Współrzędne geodezyjne (krzywoliniowe) na powierzchni elipsoidy obrotowej określane są przy pomocy dwóch współrzędnych, jest to szerokość geodezyjna

(elipsoidalna) B oraz długość geodezyjna (elipsoidalna) L. Może być również określana wysokość punktu nad powierzchnią elipsoidy jest to tzw. wysokość elipsoidalna.

Szerokość geodezyjna B – 0º - 90º (N – S) jest to kąt pomiędzy normalną do elipsoidy z płaszczyzną równika geodezyjnego. Ten zaś jest kołem powstałym w wyniku przekroju elipsoidy obrotowej płaszczyzną, do której oś obrotu elipsoidy jest prostopadła i która zawiera środek geometryczny elipsoidy O.

Poprzez przeprowadzenie kilku płaszczyzn przez oś Oz (małą półoś b) można uzyskać przekroje o kształcie elips zwanych południkami geodezyjnymi. Kąt dwuścienny pomiędzy płaszczyzną południka początkowego zawierającego oś Ox i płaszczyzną południka zawierającego punkt P nazywamy długością geodezyjną L - 0° ± 180° (E – W). Południk geodezyjny jest linią stałej długości L= const. Linia stałej szerokości geodezyjnej (równoleżnik geodezyjny) B = const. jest kołem, którego płaszczyzna jest prostopadła do osi Oz. Równoleżnik, dla którego B = 0, to równik.

Promień równoleżnika łatwo wyliczymy ze współrzędnych prostokątnych, rzutując punkt P na płaszczyznę równika

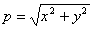
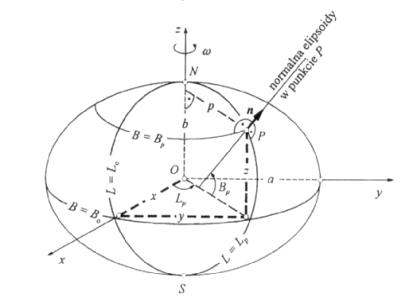
Rys. 2 Układ współrzędnych geodezyjnych i współrzędnych prostokątnych

3. Układ współrzędnych astronomicznych geograficznych

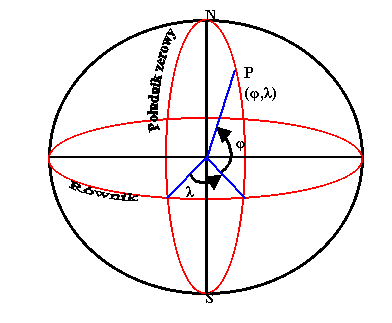
Początek układu współrzędnych astronomicznych znajduje się w środku mas Ziemi. Za pomocą szerokości astronomicznej j_A i długości astronomicznej l_A. można określić położenie punktu P na powierzchni Ziemi.

Szerokością astronomiczną punktu P nazywamy kąt j_A pomiędzy kierunkiem działania siły ciężkości (linii pionu), a płaszczyzną równika.

Natomiast długością astronomiczną punktu P nazywamy kąt dwuścienny l_A zawarty pomiędzy płaszczyzną południka zerowego i płaszczyzną południka przechodzącego przez punkt P.

Za południk zerowy przyjęto południk przechodzący przez obserwatorium astronomiczne w Greenwich. Szerokość astronomiczną j_A liczymy od równika (0°) do bieguna północnego (+90° lub 90°N) oraz do bieguna południowego (-90° lub 90°S). Natomiast długość astronomiczną liczymy od południka zerowego (0°) na wschód do180° („+” lub E) i na zachód 180° („ –„ lub W).

Rys. 3 Układ współrzędnych astronomicznych geograficznych

4. Układ współrzędnych prostokątnych przestrzennych (X, Y, Z)

Początek układu współrzędnych prostokątnych X, Y, Z pokrywa się ze środkiem geometrycznym elipsoidy odniesienia. Układ ten charakteryzuje się tym, że płaszczyzna XY pokrywa się z płaszczyzną równika; oś X leży w płaszczyźnie południka zerowego; oś Y dopełnia do układu lewoskrętnego; oś Z pokrywa się z osią obrotu Ziemi lub jest do niej równoległa,

Układ współrzędnych prostokątnych wykorzystuje się w mechanice nieba, kartografii, geodezji, zwłaszcza zadań związanych z wykorzystaniem sztucznych satelitów Ziemi

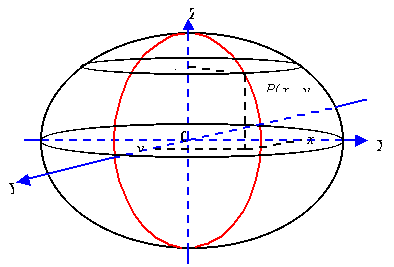
Rys. 4 Układ współrzędnych prostokątnych X, Y, Z przestrzennych

5. Układ współrzędnych geocentrycznych

Jedną ze współrzędnych w tym układzie jest długość geocentryczna λ, a drugą współrzędną szerokość geocentryczna Ψ.

Szerokość geocentryczna Ψ punktu P jest to kąt pomiędzy promieniem wodzącym r punktu P i płaszczyzną równika.

* Środek mas Ziemi

Rys. 5 Układ współrzędnych geocentrycznych

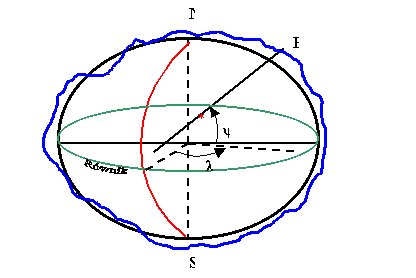
6. Układ współrzędnych zredukowanych

Jedną ze współrzędnych jest długość geograficzna λ, druga to szerokość zredukowana Φ.

Szerokość zredukowaną Φ określa kąt zawarty pomiędzy promieniem OPK i płaszczyzną równika.

Kąt ten tworzymy wykreślając ze środka układu O okrąg o promieniu równym dużej półosi a. Prostopadłą z punktu P do wielkiej osi elipsy południkowej przedłużamy do góry, aż do przecięcia z wykreślonym okręgiem w punkcie PK.

Rys. 6. Układ współrzędnych zredukowanych